There are analytical solutions for this
A simple NEC 2 model was created of two dipoles in free space. The length of the dipoles was adjusted to make one resonant, when the other was opencircuited at the feed.
Here's the feedpoint impedance as the spacing is varied, with the second dipole open. The thumbnails are small for fast loading. Click them for a much bigger version (about 25kB)
Note that the second dipole, though open, does have an effect on the feed point impedance of the first dipole. It kind of looks like as it moves far away, the reactance is about 2 ohms. I set the length so the reactance would be zero at 0.05 spacing (which is quite close)
And, here's the feedpoint impedance with the other element feedpoint shorted:
The mutual impedance has a large effect at short distances, eventually going away as you get farther away, as you would expect.
We can convert these open and shorted measurements to self and mutual impedances by using some arithmetic manipulation.
Given:
Ro,Xo = Impedance with other element open
Rs,Xs = Impedance with other element shorted
We get:
Some observations
Considering just the mutual impedance (i.e. the voltage induced in one element by the current in another), and looking at the curves of the real and imaginary components, it looks like maybe it's worth considering it in terms of magnitude and phase. After all, from a conceptual standpoint, you'd expect the magnitude to fall off as a functionof distance, and the phase to be somehow related to the time delay for the EM to propagate from one element to the other.
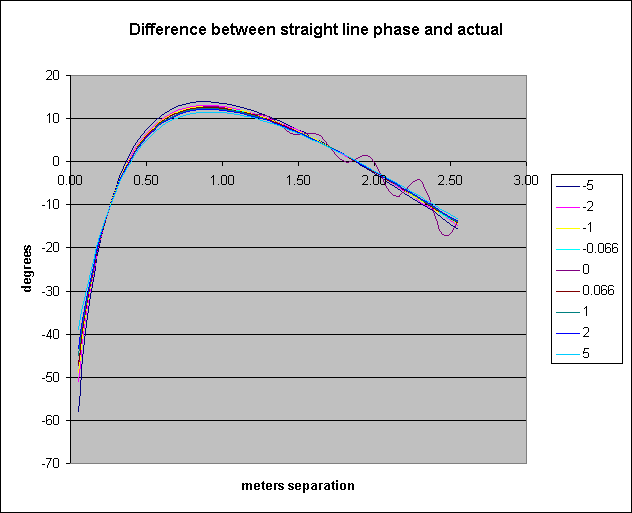
In the "far field", this would certainly be the case, and, in fact, Carter, among others, derived some standard relationships for this. However, in the near field, it's not so simple. I calculated the phase, and then fit a straight line to the phase vs distance. The difference between the straight line phase and the actual phase is shown in the figure below. The various traces are for frequencies varying from the nominal. Once you get more than a wavelength spacing (1.00) the residual settles down to a straight line, but in close, there's quite a bit of error. I'm not sure what the wiggles in the 0 frequency offset case are all about.