The purpose of this section is to get an awareness of the distance traveled by a flare or other object such as a bomb, which is jettisoned or dropped by an aircraft. This will give the reader an appreciation for the significance of aircraft tactical altitude.
From Newton's second law of motion:
| F = moa | where: |
F = Force mo = Mass of object a = Acceleration |
and the law of gravitation: ![]() ("G" is
also used instead of "K" in some references)
("G" is
also used instead of "K" in some references)
| where: |
|
|
| F = Force of attraction |
|
|
| K = universal gravitational constant |
|
|
| mo, me= Masses (not weight) of object & earth |
|
|
| r = distance between center of gravity of objects |
|
|
Combining the two equations and solving for "a" :
![]() , the familiar constant acceleration due
to gravity.
, the familiar constant acceleration due
to gravity.
Since K and me are fixed and the variation in r (the distance from the earth's center) is small except for satellites, "g" is considered fixed at 32.2 ft/sec2.
For objects with a constant acceleration (g), it can be shown that:
|
|
where: |
d = distance traveled vi = Initial velocity t = time a = acceleration = "g" |
For a falling object, Figure 1 may be used to estimate time/distance values.
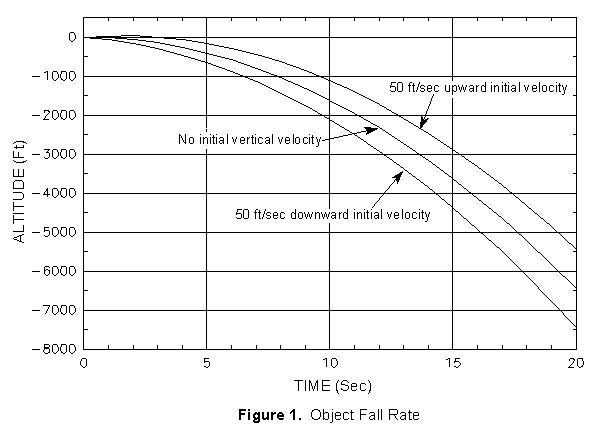
Notes:
SAMPLE CALCULATIONS:
Let us assume that we want to know how far a bomb or other object has fallen after 13 seconds if it had been dropped from an aircraft traveling at 450 kts which was in a 40 degree dive.
Our initial vertical velocity is: 450 kts (Sin 40°) (1.69 ft/sec per knot) = 489 ft/sec downward
d = Vit + 1/2at2 = -489(13) + 1/2(-32.2)(13)2 = - 6355 - 2721 = -9,076 ft.
Remember to keep the signs (+/-) of your calculations in agreement with whatever convention you are using. Gravity pulls downward, so we used a minus sign for "a" (acceleration). Also the initial velocity was downward.
In reality, any object may well have reached terminal velocity before the time indicated using the above formula or Figure 1. In this example, the actual distance determined from ballistics tables would have been 8,000 ft, which is about 13% less than the above calculation would indicate. The drag characteristics of the object determine how much shorter the distance will be. In any case, it will not have dropped farther.
Tactical aircraft carry stores in various combinations depending upon the mission. Each store has a different drag load which affects range. The pilot needs to know the total drag load in order to determine his aircraft range on a particular mission. Adding up the total drag in pounds of force for wind resistance would be cumbersome. Therefore, the drag of the stores is compared to a known reference drag (usually the aircraft), and expressed as a percentage of aircraft drag multiplied by some constant. This ratio is variously called drag count, drag index, or drag points. For instance, if a missile has 100 pounds of drag and the reference aircraft drag is 50,000 pounds, the ratio is 100/50,000 = 0.002. Multiply this by a constant of 100 (for example) and the drag index point is 0.2. The pilot only needs to look on a chart to see what the drag index points are for his stores, add up the drag points, and look on a chart to see what his aircraft range and best range (or endurance) speed will be.