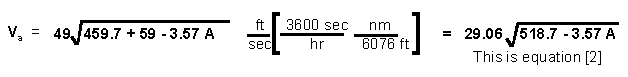MACH NUMBER and AIRSPEED vs ALTITUDE

Since the temperature and density of air decreases with altitude, so does the speed of sound, hence a given true velocity results in a higher MACH number at higher altitudes.

AIRSPEED is a term that can be easily confused. The unqualified term airspeed can mean any of the following:

1. Indicated airspeed (IAS) - the airspeed shown by an airspeed indicator in an aircraft. Indicated airspeed is expressed in knots and is abbreviated KIAS.
2. Calibrated airspeed (CAS) - indicated airspeed corrected for static source error due to location of pickup sensor on aircraft. Calibrated airspeed is expressed in knots and is abbreviated KCAS. Normally it doesn't differ much from IAS.
3. True airspeed (TAS) - IAS corrected for instrument installation error, compressibility error, and errors due to variations from standard air density. TAS is expressed in knots and is abbreviated KTAS. TAS is approximately equal to CAS at sea level but increases relative to CAS as altitude increases. At 35,000 ft, 250 KIAS (or KCAS) is approximately 430 KTAS.

Figures 1 and 2 depict relations between CAS and TAS for various altitudes and non-standard temperature conditions. The first graph depicts lower speed conditions, the second depicts higher speeds.

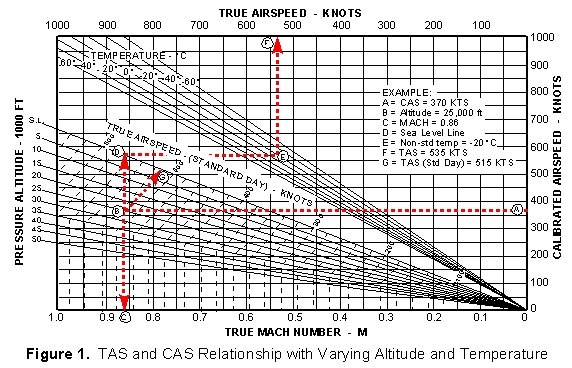
As an example of use, consider figure 1. Assume we are in the cockpit, have read our IAS from the airspeed indicator, and have applied the aircraft specific airspeed correction to obtain 370 KCAS. We start at point "A" and go horizontally to our flight altitude at point "B" (25,000 ft in this case). To find our Mach, we go down vertically to point "C" to obtain 0.86 Mach. To get our TAS at our actual environmental conditions, we go from point "B" vertically until we hit the Sea Level (S.L.) reference line at point "D", then travel horizontally until we reach our actual outside air temperature (-20° C at altitude) at point "E", then go up vertically to read our actual TAS from the scale at point "F" (535 KTAS). If we wanted our TAS at "standard" temperature and pressure conditions, we would follow the dashed lines slanting upward from point "B" to point "G" and read 515 KTAS from the scale. Naturally, we could go into the graph at any point and go "backwards" to find CAS from true Mach or TAS.

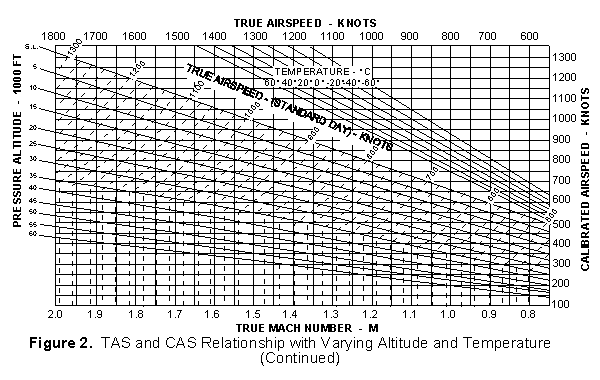
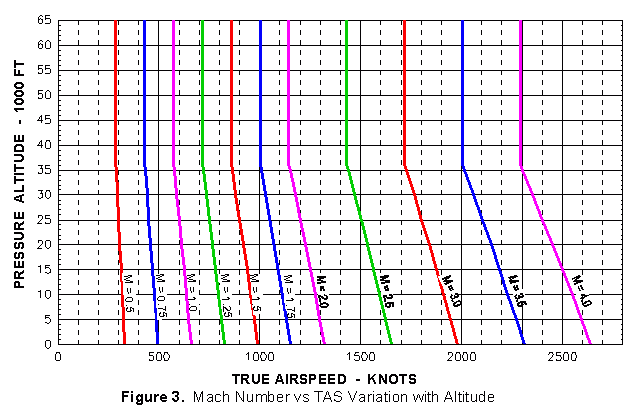
Figure 3 shows a much wider range of Mach numbers. It contains only TAS and Mach, since aircraft generally do not fly above Mach 2, but missiles (which don't have airspeed indicators) do.

The data on this graph can be obtained directly from the following formula for use at altitudes of 36,000 ft and below:

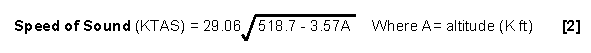
The speed of sound calculated from this formula can be used with equation [1] to obtain Mach number. This equation uses the standard sea level temperature of 59° F and a lapse rate of -3.57°/1000 ft altitude. Temperature stabilizes at -69.7° F at 36,000 ft so the speed of sound stabilizes there at 573 knots.

The following is a derivation of equation [2] for the speed of sound:

Given:
p = pressure (lb/ft²)
T = absolute temperature (° Rankine) = ° F + 459.7
v = specific volume (ft³/lb)
w = specific weight (lb/ft³) = 1/v
R = a constant (for air: R = 53.3)
= density = w/g = 1/gv therefore: v = 1/g

From Boyle's law of gasses: pv = RT , therefore we have: p/ = gRT = (32.2)(53.3)T = 1718 T [3]

It can also be shown that: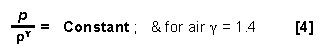

From the continuity equation applied to a sound wave: 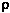AV_a = (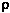+dp)A(V_a + dV_a) [5]

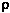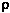
Expanding and dropping insignificant terms gives: dV_a = -V_a d / [6]

Using Newton's second law (p + 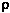V_a/2 = a constant) and taking derivatives: dp = -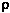V_a dV_a

substituting into [6] gives: V_a ² = dp/d 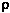[7]

Then taking derivatives of [4] and substituting in [7] gives: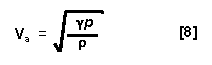

Then using [3] gives: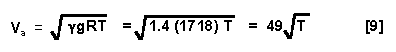

Using a "Standard" atmosphere of 59° F @ Sea Level (S.L.) and a lapse rate of -3.57°/1000 ft altitude: