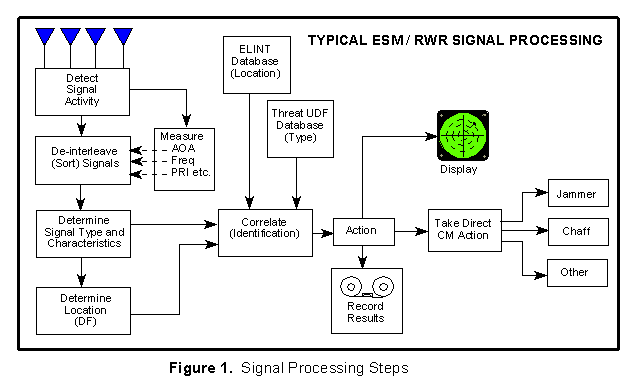
As shown in Figure 1, signal processing is basically a problem of signal detection, emitter parameter measurement and correlation, emitter sorting, identification, and operator notification. The ultimate goal of this processing is to classify radar signals by their unique characteristics and to use this data to identify enemy radars operating in the environment, determine their location or direction, assess their threat to friendly forces, and display this information to the operator.
While not all electronic support measures (ESM) or radar warning receiver (RWR) systems perform every step in this process, each completes some of them. For example, ESM systems seldom initiate direct CM action, while RWRs sometimes do. Also ESM systems frequently record electronic data for future use, but few RWRs do. ESM systems place more emphasis on accurate emitter location and hence direction finding capabilities, while RWRs usually give a rough estimate of position/distance.
The typical emitter characteristics that an ESM system can measure for a pulse radar include the following data:
However, this list is not comprehensive. Other emitter parameters are available which may be necessary to characterize the threat system.
More sophisticated ESM systems can measure additional parameters, such as PRI modulation characteristics, inter-and intra-pulse Frequency Modulation (FM), missile guidance characteristics (e.g., pattern of pulse spacing within a pulse group), and Continuous Wave (CW) signals.
Still other parameters which can describe an electromagnetic wave but are currently not commonly used for identification include polarization and phase. However, as threat emitters begin to use this data more frequently to avoid jamming the more important they may become in identifying signals.
Some of the emitter characteristics which describe an electromagnetic wave are shown in Figure 2.
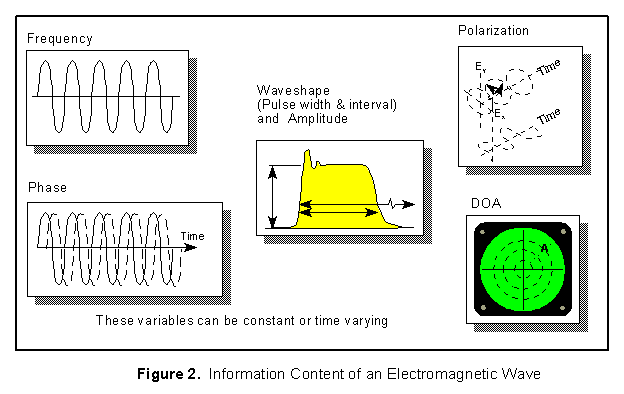
Table 1 illustrates the relative importance of several measured parameters during various stages of signal processing.
| Parameter |
|
|
|
|
Frequency Amplitude Angle of Arrival TOA PRI PRI type PW Scan rate and type Lobe Duration |
|
|
|
 0 = Not Useful 1 = Some Use 2
= Very Useful |
|||
Some emitter parameters can be measured using a single pulse; these parameters are referred to as monopulse parameters. The monopulse parameters include RF, PW, DOA, amplitude and TOA. RF can be determined on a pulse-by-pulse basis by receivers that can measure frequency. Frequency is very useful for emitter identification since most radars operate at a single frequency. Most real-time systems measure pulse width instead of pulse shape because the latter is much more difficult to characterize mathematically. Unfortunately, the apparent pulse width can be severely distorted by reflections, and consequently, its usefulness for emitter identification is limited. DOA cannot be used for emitter identification, but is excellent for sorting signals. A number of ESM systems use both frequency and DOA information to distinguish the new signals from the old (that is, known) ones. Amplitude also cannot be used for emitter identification. However, it can be used for sorting and for gross distance estimation using precompiled emitter's effective radiated power. Moreover, amplitude in conjunction with TOA can be used to determine the emitter's scan characteristics.
Other emitter parameters such as PRI, guidance and scan characteristics can be determined only by analyzing a group of pulses. All these parameters are useful for emitter identification; unfortunately, they require time for data collection and analysis, and call for sophisticated signal processing algorithms.
The problem of signal recognition in real-time is complicated by two factors: modulation of the signals and the very high pulse densities expected in the environment. Complex modulations (for example, inter-pulse RF modulation, intra-pulse RF modulation and agile Pulse Repetition Frequencies (PRFs)) present a significant pattern recognition problem for a number of ESM systems. It is expected that during some missions, hundreds of emitters will be transmitting simultaneously in the same vicinity. Wide-open antenna/receiver combination systems may have to cope with up to a million PPS. Even narrow-band receivers can expect data rates up to 100,000 PPS. At these rates, a single modern computer cannot be expected to process all the pulses, derive the characteristics for all emitters and identify the emitters in real-time. Other factors which encumber signal recognition include missing pulses, atmospheric noise and multiple reflections of pulses.
Present RWRs are designed primarily to cope with stable emitters. A stable emitter is one whose frequency and pulse repetition interval (PRI) remain relatively constant from pulse to pulse. The future threat will move steadily away from the stable emitter towards agile emitters which vary their frequency and PRI characteristics. The first change in this direction is towards the patterned agile emitter which varies its pulse and frequency parameters in accordance with a specific pattern. Examples of patterned agile emitters are MTI radars which use staggered PRFs, pulse Doppler radars which change frequency and PRF on a block-to-block basis, and certain frequency-agile radars whose transmitter frequency is mechanically modulated in a systematic pattern (e.g., spin-tuned magnetron). The next step in this evolution is towards truly agile emitters which change their frequency and PRF in a random manner on a pulse-to-pulse basis. One tempering factor in this evolution is that radars which process Doppler must maintain a constant frequency for at least two consecutive pulses.
In addition to agile frequency and PRI parameters, the future threat will be composed of a number of high-PRF pulsed Doppler, burst-frequency, CW, pulse-compression, agile-beam, and LPI radars, which use pseudo-noise waveforms. This conglomeration of radar types will cause a high signal density which must be segmented into a manageable data stream by the use of both frequency and spatial filtering in the RWR. While frequency and PRI are good parameters for sorting present-day non-agile emitters, they are poor or useless parameters for sorting agile emitters.
|
|
PASSIVE DIRECTION FINDING AND EMITTER LOCATION
Direction finding (DF) systems provide several important functions in modern EW systems. We have already discussed the importance of measuring the emitter's bearing, or angle of arrival (AOA), as an invariant sorting parameter in the deinterleaving of radar signals and in separating closely spaced communication emitters. In addition, the conservation of jamming power in power-managed ECM systems depends on the ability of the associated ESM system to measure the direction to the victim emitter. A function which is becoming increasingly important in defense suppression and weapon delivery systems involves locating the emitter's position passively. This can be accomplished from a single moving platform through successive measurements of the emitter's angular direction, or from multiple platforms which make simultaneous angular measurements.
The emitter identification function requires identifying and associating consecutive pulses produced by the same emitter in angle of arrival (AOA) and frequency. The AOA is a parameter which a hostile emitter cannot change on a pulse-to-pulse basis. However, to measure the AOA of pulses which overlap in the time domain first requires them to be separated in the frequency domain. The advanced ESM receivers which accomplish this function must operate over several octaves of bandwidth while providing RMS bearing accuracies on the order of at least 2 degrees with high POI and fast reaction time in dense signal environments.
There are basically three methods, depicted in
Figure 3, which allow the passive location of stationary ground-based
emitters from airborne platforms. These are:
1. The azimuth triangulation method where the intersection of successive spatially displaced bearing measurements provides the emitter location;
2. The azimuth/elevation location technique, which provides a single-pulse instantaneous emitter location from the intersection of the measured azimuth/elevation line with the earth's surface; and
3. The time difference of arrival (TDOA), or precision emitter location system (PELS) method, which measures the difference in time of arrival of a single pulse at three spatially remote locations.
Additional methods include:
1. Phase rate of change, which is similar to triangulation, except it makes calculations using the phase derivative.
2. Angle distance techniques, where the distance from the emitter is derived from the signal strength (with known "threat" characteristics).
3. RF Doppler processing, which measures Doppler changes as the aircraft varies direction with respect to the "target" radar.
The relative advantages and disadvantages of each are given in Table 2.
| Measurement Technique | Advantages | Disadvantages |
| Triangulation | Single Aircraft |
Non-Instantaneous Location; Inadequate Accuracy for Remote Targeting; Not Forward Looking |
| Azimuth/Elevation |
Single Aircraft; Instantaneous Location Possible |
Accuracy Degrades Rapidly at Low Altitude; Function of Range |
| Time Difference of Arrival (Pulsed Signals) |
Very High Precision, Can Support Weapon Delivery Position Requirements Very Rapid, Can Handle Short On-Time Threat |
Very Complex, At Least 3 Aircraft; High Quality Receivers; DME (3 Sites); Very Wideband Data Link; Very High Performance Control Processor; Requires Very High Reliability Subsystems. Requires common time reference and correlation operation for non-pulse signals. |
The triangulation method has the advantage of using a single aircraft, and its accuracy is greatest for a long baseline and the broadside geometry. The accuracy degenerates as the aircraft heading line approaches the boresight to the emitter.
The azimuth/elevation technique also has the advantage of using a single aircraft, but suffers from the difficultness of making an accurate elevation measurement with limited vertical aperture and in the presence of multipath effects.
The TDOA technique requires multiple aircraft and is complex, but has high potential accuracy. The determination of the location of the site involves the solution of at least two simultaneous second order equations for the intersection of two hyperbolas which represent T2 - T1 = Constant #1 and T3 - T2 = Constant #2. This method can be used to obtain a fix for an emitter which radiates only a single pulse.
ANGLE-OF-ARRIVAL (AOA) MEASUREMENTS
Several of the above DF measurements require AOA determination. Threat AOA measurements are also required to inform the aircrew in order to position the aircraft for optimal defense.
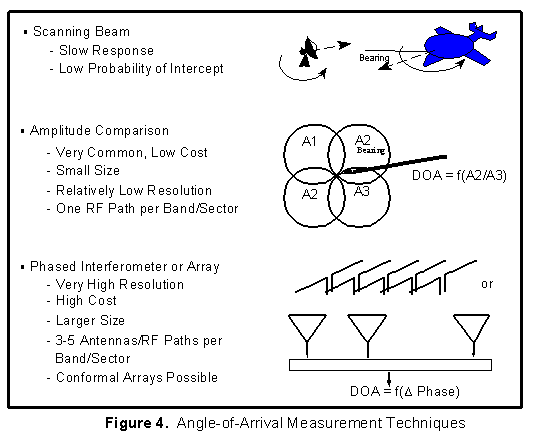
As shown in Figure 4, angle-of-arrival measuring systems fall into three main system categories of:
Scanning Beam
The mechanically scanning beam, or "spinner," requires only a single receiver and also exhibits high sensitivity due to the use of a directive antenna. The disadvantage is that the "spinner" usually exhibits slow response because it must rotate through the coverage angle (e.g., 360 degrees) to ensure that it intercepts an emitter. Also, if the emitter uses a scanning directional antenna, both beams must point at each other for maximum sensitivity, which is a low probability occurrence. Both of these effects cause the mechanically scanning beam technique to have a low probability of intercept (POI).
Amplitude Comparison
The two primary techniques used for direction finding are the amplitude-comparison method and the interferometer or phase-comparison method. The phase-comparison method generally has the advantage of greater accuracy, but the amplitude-comparison method is used extensively due to its lower complexity and cost. Regardless of which technique is used, it should be emphasized that the ultimate rms angular accuracy is given by:
Thus, phase interferometers that typically use very widebeam antennas require high signal-to-noise ratios to achieve accurate angle-of-arrival measurements. Alternately, a multi-element array antenna can be used to provide relatively narrow interferometer lobes, which require modest signal-to-noise ratios.
Virtually all currently deployed radar warning receiving (RWR) systems use amplitude-comparison direction finding (DF). A basic amplitude-comparison receiver derives a ratio, and ultimately angle-of-arrival or bearing, from a pair of independent receiving channels, which utilize squinted antenna elements that are usually equidistantly spaced to provide an instantaneous 360 ° coverage. Typically, four or six antenna elements and receiver channels are used in such systems, and wideband logarithmic video detectors provide the signals for bearing-angle determination. The monopulse ratio is obtained by subtraction of the detected logarithmic signals, and the bearing is computed from the value of the ratio.
Amplitude comparison RWRs typically use broadband cavity-backed spiral antenna elements whose patterns can be approximated by Gaussian-shaped beams. Gaussian-shaped beams have the property that the logarithmic output ratio slope in dB is linear as a function of angle of arrival. Thus, a digital look-up table can be used to determine the angle directly. However, both the antenna beamwidth and squint angle vary with frequency over the multi-octave bands used in RWRs. Pattern shape variations cause a larger pattern crossover loss for high frequencies and a reduced slope sensitivity at low frequencies. Partial compensation of these effects, including antenna squint, can be implemented using a look-up table if frequency information is available in the RWR. Otherwise, gross compensation can be made, depending upon the RF octave band utilized.
Typical accuracies can be expected to range from 3 to 10 degrees rms for multi-octave frequency band amplitude-comparison systems which cover 360 degrees with four to six antennas.
The four-quadrant amplitude-comparison DF systems employed in RWRs have the advantage of simplicity, reliability, and low cost. Usually, only one antenna per quadrant is employed which covers the 2 to 18 GHz band. The disadvantages are poor accuracy and sensitivity, which result from the broad-beam antennas employed. Both accuracy and sensitivity can be improved by expanding the number of antennas employed. For example, expanding to eight antennas would double the accuracy and provide 3 dB more gain. As the number of antennas increases, it becomes appropriate to consider multiple-beam-forming antennas rather than just increasing the number of individual antennas. The geometry of multiple-beam-forming antennas is such that a conformal installation aboard an aircraft is difficult. Therefore, this type of installation is typically found on naval vessels or ground vehicles where the space is available to accommodate this type of antenna.
Simultaneous-multiple-beam (amplitude comparison)
The simultaneous-multiple-beam system uses an antenna, or several antennas, forming a number of simultaneous beams (e.g., Butler matrix or Rotman lens), thereby retaining the high sensitivity of the scanning antenna approach while providing fast response. However, it requires many parallel receiving channels, each with full frequency coverage. This approach is compatible with amplitude-monopulse angular measuring techniques which are capable of providing high angular accuracy.
A typical example of a multiple-beam antenna is a 16-element circular array developed as part of a digital ESM receiver. This system covers the range from 2 to 18 GHz with two antenna arrays (2 to 7.5 GHz and 7.5 to 18 GHz), has a sensitivity of -55 to -60 dBm and provides an rms bearing accuracy of better than 1.7 degrees on pulsewidths down to 100 ns.
Phased Interferometer Techniques
The term interferometer generally refers to an array type antenna in which large element spacing occurs and grating lobes appear.
Phase interferometer DF systems are utilized when accurate angle-of-arrival information is required. They have the advantage of fast response, but require relatively complex microwave circuitry, which must maintain a precise phase match over a wide frequency band under extreme environmental conditions. When high accuracy is required (on the order of 0.1 to 1 ° ), wide baseline interferometers are utilized with ambiguity resolving circuitry.
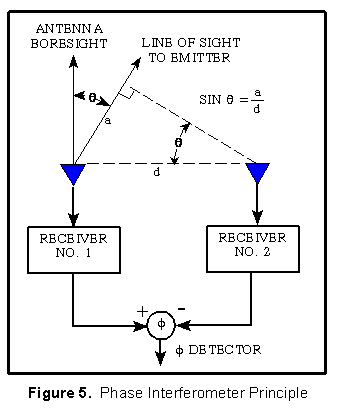
The basic geometry is depicted in Figure 5, whereby a plane wave arriving at an angle is received by one antenna earlier than the other due to the difference in path length.
The time difference can be expressed as a phase difference:
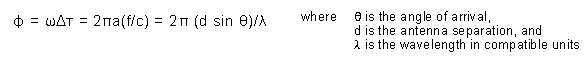
The unambiguous field of view (FOV) is given by 
= 2
sin-1 (
/2d), which for 
/2 spacing results
in 180 ° coverage. This spacing must be established for the
highest frequency to be received.
Interferometer elements typically use broad antenna beams with beamwidths on the order of 90 °. This lack of directivity produces several adverse effects. First, it limits system sensitivity due to the reduced antenna gain. Secondly, it opens the system to interference signals from within the antenna's broad angular coverage. The interference signals often include multipath from strong signals which can limit the accuracy of the interferometer.
In an interferometer, the locus of points that produce the same time or phase delay forms a cone. The indicated angle is the true azimuth angle multiplied by the cosine of the elevation angle. The error in assuming the incident angle to be the azimuth angle is negligible for signals near the antenna's boresight. At 45 ° azimuth and 10 ° elevation, the error is less than 1 °, increasing to 15 ° for both at 45 °. Two orthogonal arrays, one measuring the azimuth angle and the other the elevation angle can eliminate this error. For targets near the horizon, the depression angle is small, thereby requiring only horizontal arrays.
The rms angular accuracy of an interferometer in radians is given by:
For a two-element interferometer, the spacing (d) must be /2
or less to provide unambiguous, or single lobe +/- 90 °, coverage.
This, in effect, sets a wide interferometer (or grating) lobe
which must be split by a large factor to achieve high accuracy.
This, in turn, imposes a requirement for high SNR to achieve the
large beam-splitting factor. For example, if 0.1 ° accuracy
is required from an unambiguous two-element interferometer, then
a SNR of about 50 dB is required to achieve this accuracy. This
may be difficult to achieve considering the inherently low sensitivity
of an interferometer system.
When high accuracy is required from an interferometer system,
it is usual to employ separations greater than /2. The
increased separation sets up a multi-grating-lobe structure through
the coverage angle which requires less SNR to achieve a specified
accuracy. For example, a two-element interferometer with 16
spacing would set up a 33-grating-lobe structure (including the
central lobe) throughout the +/- 90 ° coverage angle. Within
each of the 33 grating lobes, it would only require a SNR on the
order of 20 dB to achieve 0.1 ° accuracy. However, there would
be 33 ambiguous regions within the +/- 90 ° angular coverage
and also 32 nulls (where the phase detector output is zero), about
which the system would be insensitive to an input signal. The
ambiguities could be resolved by employing a third antenna element
with /2 spacing, which would provide an accuracy on
the order of 3 ° with 20 dB SNR. This accuracy is sufficient
to identify which of the 33 lobes contains the signal. Providing
coverage in the null regions requires additional antenna elements.
Interferometers employing multiple antenna elements are called
multiple-baseline interferometers. In a typical design, the receiver
consists of a reference antenna and a series of companion antennas.
The spacing between the reference element and the first companion
antenna is /2; other secondary elements are placed to form
pairs separated by 1, 2, 4, and 8 wavelengths. The initial AOA
is measured unambiguously by the shortest-spaced antenna pair.
The next greatest spaced pair has a phase rate of change which
is twice that of the first, but the information is ambiguous due
to there being twice as many lobes as in the preceding pair. A
greater phase rate of change permits higher angular accuracy while
the ambiguity is resolved by the previous pair. Thus, the described
multiple-baseline interferometer provides a binary AOA measurement
where each bit of the measurement supplies a more accurate estimate
of the emitter's AOA.
Harmonic multiple-baseline interferometers use elements which
are spaced at 2n /2, with n = 0, 1, 2, 3. In
nonharmonic interferometers, no pair of antennas provides a completely
unambiguous reading over the complete field of view. For example,
the initial spacing in the nonharmonic interferometer might be
, while the next companion element spacing is 3/2.
Ambiguities are resolved by truth tables, and hence the accuracy
is set by the spacing of the widest baseline antenna pair. Nonharmonic
interferometers have been implemented over 9:1 bandwidths (2 to
18 GHz) with rms accuracies from 0.1 to 1 ° and with no ambiguities
over +/- 90 °. The principal advantage of the nonharmonic
over the harmonic interferometer is the increased bandwidth for
unambiguous coverage.
Interferometer DF accuracy is determined by the widest baseline
pair. Typical cavity-backed spirals, track to 6 electrical degrees,
and associated receivers track to 9 °, resulting in an rms
total of 11 °. At a typical 16 dB SNR, the rms phase noise
is approximately 9 electrical degrees. For these errors and an
emitter angle of 45 °, a spacing of 25 is required
for 0.1 ° rms accuracy while a spacing of 2.5 is needed
for 1 ° accuracy. For high accuracy, interferometer spacings
of many feet are required. In airborne applications, this usually
involves mounting interferometer antennas in the aircraft's wingtips.
The characteristics of typical airborne amplitude comparison and phase interferometer DF systems are summarized in Table 3. The phase interferometer system generally uses superheterodyne receivers which provide the necessary selectivity and sensitivity for precise phase measurements.
| Amplitude Comparison | Phase Interferometer | |
| Sensor Configuration | Typically 4 to 6 Equispaced Antenna Elements for 360 ° Coverage | 2 or more RHC or LHC Spirals in Fixed Array |
| DF Accuracy |
|
|
| DF Accuracy Improvement | Decrease Antenna BW; Decrease Amplitude Mistrack; Increase Squint Angle |
Increase Spacing of Outer Antennas; Decrease Phase Mistrack |
| Typical DF Accuracy | 3 ° to 10 ° rms | 0.1 ° to 3 ° rms |
| Sensitivity to Multipath/ Reflections | High Sensitivity; Mistrack of Several dB Can Cause Large DF Errors | Relatively Insensitive; Interferometer Can Be Made to Tolerate Large Phase Errors |
| Platform Constraints | Locate in Reflection Free Area | Reflection Free Area; Real Estate For Array; Prefers Flat Radome |
| Applicable Receivers | Crystal Video; Channelizer; Acousto-Optic; Compressive; Superheterodyne | Superheterodyne |
CdB
= Amplitude Monopulse Ratio in dB 
S = Squint Angle
in degrees BW = Antenna Beamwidth in degrees