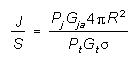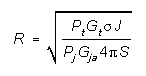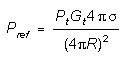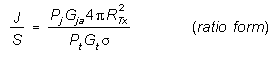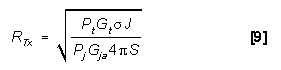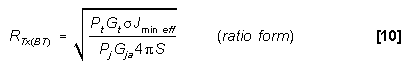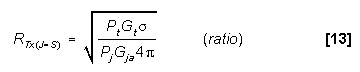BURN-THROUGH / CROSSOVER RANGE
The burn-through equations are derived in this section. These
equations are most commonly used in jammer type of applications.
The following is a summary of the important equations explored
in this section:
J/S CROSSOVER RANGE (MONOSTATIC) (J=S)
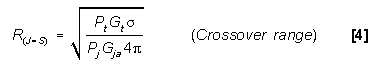 or in dB form: or in dB form:
20log RJ
= S = 10log Pt + 10log Gt + 10log  - 10log Pj - 10log Gja - 10.99 dB
- 10log Pj - 10log Gja - 10.99 dB |
If simplified radar equations developed in previous
sections are used:
20log RJ = S = 10log
Pt + 10log Gt + G - 10log Pj - 10log Gja - K1
- 20log f1
- 10log Pj - 10log Gja - K1
- 20log f1  (in dB) (in dB) |
BURN-THROUGH RANGE (MONOSTATIC)
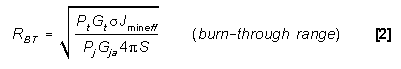 or in dB form: or in dB form:
20log RBT
= 10log Pt + 10log Gt + 10log  -
10log Pj - 10log Gja + 10log (Jmin
eff/S) - 10.99 dB -
10log Pj - 10log Gja + 10log (Jmin
eff/S) - 10.99 dB |
If simplified radar equations developed in previous
sections are used:
20log
R BT = 10log Pt + 10log Gt +
G - 10log Pj - 10log Gja
- K1 + 10log (Jmin eff/S) - 20log f1 - 10log Pj - 10log Gja
- K1 + 10log (Jmin eff/S) - 20log f1
 (in dB) (in dB) |
BURN-THROUGH RANGE (BISTATIC)
RTx
is the range from the radar transmitter to the target and is
different from RRx, which is the range from the target
to the receiver. Use monostatic equations and substitute RTx
for R |
Target gain factor;
G = 10log = 10log  +
20log f1 + K2 (in dB) +
20log f1 + K2 (in dB) |
One-way free space loss;
 Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) |
K2 Values
(dB) |
RCS ( ) )
(units)
m 2
ft 2 |
f1
in MHz
K2 =
-38.54
-48.86 |
f1
in GHz
K2 =
21.46
11.14 |
|
K1 Values
(dB) |
Range
(units)
NM
Km
m
yd
ft |
f1
in MHz
K1 =
37.8
32.45
-27.55
-28.33
-37.87 |
f1
in GHz
K1 =
97.8
92.45
32.45
31.67
22.13 |
|
CROSSOVER RANGE and BURN-THROUGH RANGE
To present the values of J and S, (or J/S) over a minimum to
maximum radar to target range of interest, equation [1], in the
Constant Power (Saturated) Jamming section
which has a slope of 20 log for J vs. range and equation [2],
in the same section, which has a slope of 40 log for S vs. range
are plotted. When plotted on semi-log graph paper, J and S (or
J/S) vs. range are straight lines as illustrated in Figure 1.
Figure 1 is a sample graph - it cannot be used for data.
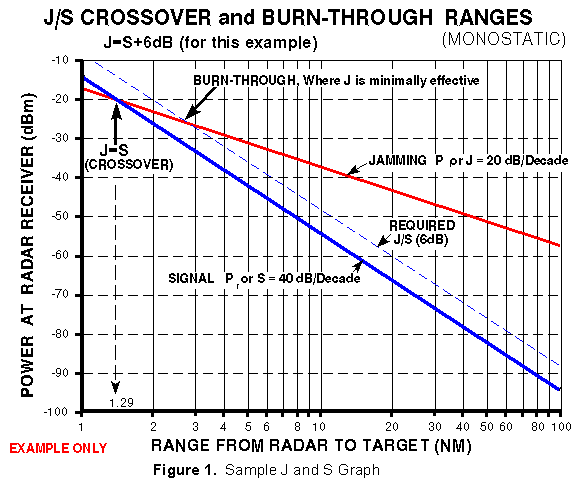
The crossing of the J and S lines (known as crossover) gives
the range where J = S (about 1.29 NM), and shows that shorter
ranges will produce target signals greater than the jamming signal.
The point where the radar power overcomes the jamming signal
is known as burn-through. The crossover point where J = S could
be the burn-through range, but it usually isn't because normally
J/S > 0 dB to be effective due to the task of differentiating
the signal from the jamming noise floor (see receiver sensitivity
section). For this example, the J/S required for the ECM to be
effective is given as 6 dB, as shown by the dotted line. This
required J/S line crosses the jamming line at about 2.8 NM which,
in this example, is the burn-through range.
|
In this particular example, we have: |
Pt = 80 dBm |
Gt = 42 dB |
|
Pj = 50 dBm |
Gja = 6 dB |
|
 = 18 m2 = 18 m2 |
f = 5.9 GHz (not necessary for all calculations) |
A radar can be designed with higher than necessary power
for earlier burn-through on jamming targets. Naturally that would
also have the added advantage of earlier detection of non-jamming
targets as well.
|
Note: To avoid having to include additional
terms for the following calculations, always combine any transmission
line loss with antenna gain. |
CROSSOVER AND BURN-THROUGH RANGE EQUATIONS (MONOSTATIC)
To calculate the crossover range or burn-through range the
J/S equation must be solved for range. From equation [3], in the
Constant Power (Saturated) Jamming section:
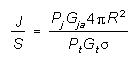 |
Solving for R: |
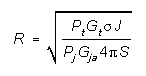 |
[1] |
BURN-THROUGH RANGE (MONOSTATIC) - Burn-through
Range (Monostatic) is the radar to target range where the target
return signal (S) can first be detected through the ECM (J). It
is usually the range when the J/S just equals the minimum effective
J/S.
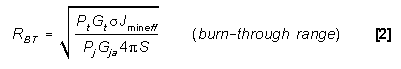
or in dB form, (using 10log 4 = 10.99 dB):
= 10.99 dB):
20log RBT = 10log Pt + 10log Gt
+ 10log  - 10log Pj - 10log Gja +
10log (Jmin eff/S) - 10.99 dB
- 10log Pj - 10log Gja +
10log (Jmin eff/S) - 10.99 dB  [3]
[3]
RANGE WHEN J/S CROSSOVER OCCURS (MONOSTATIC) - The crossover
of the jammer's 20 dB/decade power line and the skin return signal's
40 dB/decade power line of Figure 1 occurs for the case where
J = S in dB or J/S=1 in ratio. Substituting into equation [1]
yields:
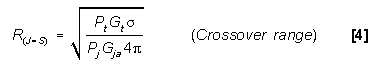
or in dB form:
20log RJ = S = 10log Pt + 10log Gt
+ 10log  - 10log Pj - 10log Gja -
10.99 dB
- 10log Pj - 10log Gja -
10.99 dB  [5]
[5]
Note: keep R and  in same units
in all equations.
in same units
in all equations.
CROSSOVER AND BURN-THROUGH EQUATIONS (MONOSTATIC)
USING  - ONE WAY FREE SPACE LOSS
- ONE WAY FREE SPACE LOSS
The other crossover burn-through range formulas can be confusing
because a frequency term is subtracted (equations [6], [7] and
[8]), but both ranges are independent of frequency. This subtraction
is necessary because when J/S is calculated directly as previously
shown,  2 or (c/f)2 terms
canceled, whereas in the simplified radar equations, a frequency
term is part of the G
2 or (c/f)2 terms
canceled, whereas in the simplified radar equations, a frequency
term is part of the G term and has to be cancelled
if one solves for R. From equation [8], in the Constant
Power (Saturated) Jamming section :
term and has to be cancelled
if one solves for R. From equation [8], in the Constant
Power (Saturated) Jamming section :
10log J/S = 10log Pj + 10log Gja - 10log
Pt - 10log Gt - G +
+ 
 (factors in dB)
(factors in dB)
or rearranging:  = 10log Pt + 10log
Gt + G
= 10log Pt + 10log
Gt + G - 10log Pj
- 10log Gja + 10log (J/S)
- 10log Pj
- 10log Gja + 10log (J/S)
from the Two-Way Radar Equation (Monostatic)
section:  = 20log f 1R1 + K1
or 20log R1 =
= 20log f 1R1 + K1
or 20log R1 =  - K1 - 20log f1
- K1 - 20log f1
then substituting for  :
:
20log R1 = 10log Pt + 10log Gt
+ G - 10log Pj - 10log Gja
- K1 + 10log (J/S) - 20log f1
- 10log Pj - 10log Gja
- K1 + 10log (J/S) - 20log f1  (factors in dB)
(factors in dB)  [6]
[6]
EQUATION FOR BURN-THROUGH RANGE (MONOSTATIC) - Burn-through
occurs at the range when the J/S just equals the minimum effective
J/S. G and K 1 are as defined at the
beginning of this section.
and K 1 are as defined at the
beginning of this section.
20log R BT = 10log Pt + 10log Gt
+ G - 10log Pj - 10log Gja
- K1 + 10log (Jmin eff/S) - 20log f1
- 10log Pj - 10log Gja
- K1 + 10log (Jmin eff/S) - 20log f1
 (factors in dB) [7]
(factors in dB) [7]
EQUATION FOR THE RANGE WHEN J/S CROSSOVER OCCURS (MONOSTATIC)
- The J/S crossover range occurs for the case where J = S, substituting
into equation [6] yields:
20log RJ = S = 10log Pt + 10log Gt
+ G - 10log Pj - 10log Gja
- K1 - 20log f1
- 10log Pj - 10log Gja
- K1 - 20log f1  (factors
in dB)
(factors
in dB)  [8]
[8]
BURN-THROUGH RANGE (BISTATIC)
Bistatic J/S crossover range is the radar-to-target range when
the power received (S) from the radar skin return from the target
equals the power received (J) from the jamming signal transmitted
from the target. As shown in Figure 6, of the J/S
Ratio - Constant Power (Saturated) Jamming Section, the receive
antenna that is receiving the same level of J and S is remotely
located from the radar's transmit antenna. Bistatic equations
[11], [13], and [14] in that section show that J/S is only a function
of radar to target range, therefore J/S is not a function of wherever
the missile is in its flight path provided the missile is in the
antenna beam of the target's jammer. The missile is closing on
the target at a very much higher rate than the target is closing
on the radar, so the radar to target range will change less during
the missile flight.
It should be noted that for a very long range air-to-air missile
shot, the radar to target range could typically decrease to 35%
of the initial firing range during the missile time-of-flight,
i.e. A missile shot at a target 36 NM away, may be only 12 NM
away from the firing aircraft at missile impact.
Figure 2 shows both the jamming radiated from the target and
the power reflected from the target as a function of radar-to-target
range.
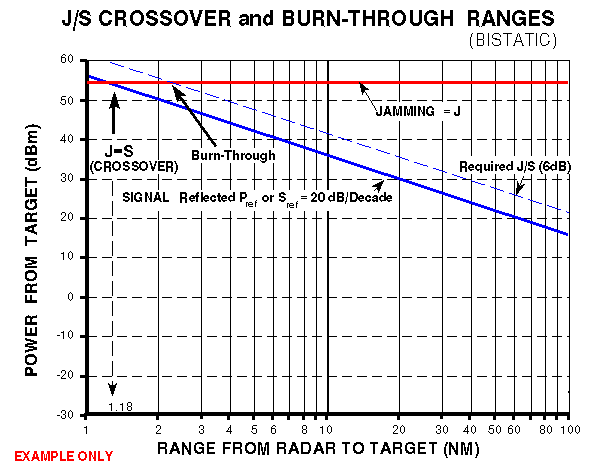
In this particular example, the RCS is assumed to be smaller,
15 m2 vice 18m2 in the monostatic case,
since the missile will be approaching the target from a different
angle. This will not, however, always be the case.
In this plot, the power reflected is: 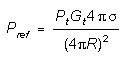
Substituting the values given previously in the example, we
find that the crossover point is at 1.18 NM (due to the assumed
reduction in RCS).
CROSSOVER AND BURN-THROUGH RANGE EQUATIONS (BISTATIC)
To calculate the radar transmitter-to-target range where J/S
crossover or burn-through occurs, the J/S equation must be solved
for range. From equation [11] in J/S Ratio
- Constant Power (Saturated) Jamming Section, :
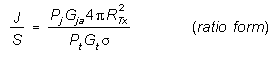
Solving for RTx:
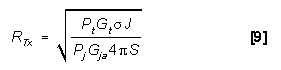
Note: Bistatic equation [10] is identical to monostatic equation
[1] except RTx must be substituted for R and a bistatic
RCS ( ) will have to be used since RCS varies with aspect
angle. The common explanations will not be repeated in this section.
) will have to be used since RCS varies with aspect
angle. The common explanations will not be repeated in this section.
BURN-THROUGH RANGE (BISTATIC) - Burn-through
Range (Bistatic) occurs when J/S just equals the minimum effective
J/S. From equation [9]:
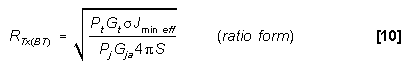
or in dB form:
20log RTx(BT) = 10log Pt + 10log Gt
+ 10log  - 10log Pj - 10log Gja +
10log (Jmin eff/S) - 10.99 dB
- 10log Pj - 10log Gja +
10log (Jmin eff/S) - 10.99 dB  [11]
[11]
If using the simplified radar equations (factors in dB):
20log RTx(BT) = 10log Pt + 10log Gt
+ G - 10log Pj - 10log Gja
- K1 + 10log (Jmin eff/S) - 20log f1
- 10log Pj - 10log Gja
- K1 + 10log (Jmin eff/S) - 20log f1
 [12]
[12]
Where G and K1 are defined at the beginning
of the section.
and K1 are defined at the beginning
of the section.
RANGE WHEN J/S CROSSOVER OCCURS (BISTATIC) - The crossover
occurs when J = S in dB or J/S = 1 in ratio.
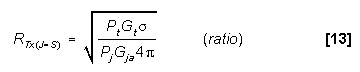
or in log form:
20log RTx(J=S) = 10log Pt + 10log Gt
+ 10log  - 10log Pj - 10log Gja -
10.99 dB
- 10log Pj - 10log Gja -
10.99 dB  [14]
[14]
If simplified equations are used (with G and K1 as defined at the beginning of this section)
we have:
and K1 as defined at the beginning of this section)
we have:
20log RTx(J=S) = 10log Pt + 10log Gt
+ G - 10log Pj - 10log Gja
- K1 - 20log f1
- 10log Pj - 10log Gja
- K1 - 20log f1  (factors
in dB)
(factors
in dB)  [15]
[15]
Note: keep R and  in same units in all equations.
in same units in all equations.
DETAILS OF SEMI-ACTIVE MISSILE J/S
Unless you are running a large scale computer simulation that
includes maneuvering, antenna patterns, RCS, etc., you will seldom
calculate the variation in J/S that occurs during a semi-active
missile's flight. Missiles don't fly straight lines at constant
velocity. Targets don't either - they maneuver. If the launch
platform is an aircraft, it maneuvers too. A missile will accelerate
to some maximum velocity above the velocity of the launch platform
and then decelerate.
The calculation of the precise variation of J/S during a missile
flight for it to be effective requires determination of all the
appropriate velocity vectors and ranges at the time of launch,
and the accelerations and changes in relative positions during
the fly out. In other words, it's too much work for too little
return.
The following are simplified examples for four types of intercepts.
|
In these examples, all velocities are constant, and are all
along the same straight line. The missile velocity is 800 knots
greater than the launch platform velocity which is assumed to
be 400 kts. The missile launch occurs at 50 NM.
For the AAM tail chase, the range from the radar to the target
remains constant and so does the J/S. In these examples
the maximum variation from launch J/S is +/- 6 dB. That represents
the difference in the radar to target range closing at very high
speed (AAM head on) and the radar to target range opening at
moderate speed (SAM outbound target). The values shown above
are examples, not rules of thumb, every intercept will be different. |
|
J/S (dB) |
 J/S (dB) J/S (dB) |
|
At Launch: |
29 |
n/a |
|
Intercept Type |
At 2 sec. to Intercept: |
|
AAM Head-on: |
23 |
-6 |
|
SAM Incoming Target: |
25 |
-4 |
|
AAM Tail Chase: |
29 |
0 |
|
SAM Outbound Target: |
35 |
+6 |
|
Even for the simplified linear examples shown, graphs of the
J and S will be curves - not straight lines. Graphs could be plotted
showing J and S vs. radar to target range, or J and S vs. missile
to target range, or even J/S vs. time of flight. If the J/S at
launch is just barely the minimum required for effectiveness,
and increasing it is difficult, then a detailed graph may be warranted,
but in most cases this isn't necessary.
Return to: EW
& Radar Handbook Home Page | Table
of Contents
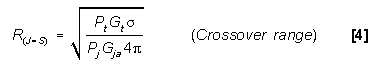 or in dB form:
or in dB form: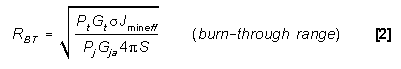 or in dB form:
or in dB form: