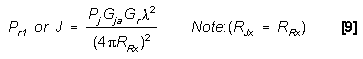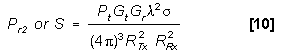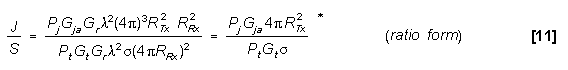JAMMING TO SIGNAL (J/S) RATIO
CONSTANT POWER [SATURATED] JAMMING
The following table contains a summary of the equations
developed in this section.
JAMMING TO SIGNAL (J/S) RATIO (MONOSTATIC)
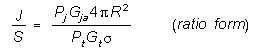  or: or:
10log J/S = 10log Pj+ 10log Gja - 10log
Pt - 10log Gt - 10log  +
10.99 dB + 20log R +
10.99 dB + 20log R
Note (1): Neither f nor 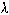 terms
are part of the final form of these equations. terms
are part of the final form of these equations. |
If simplified radar equations developed in previous
sections are used:
10log (J/S) = 10log Pj + 10log Gja - 10log
Pt - 10log Gt - G +
+  (in dB) (in dB)
Note (2): The 20log f 1 term in -G cancels the 20log f 1 term in
cancels the 20log f 1 term in  . . |
JAMMING TO SIGNAL (J/S) RATIO (BISTATIC)
RTx is the range from the radar transmitter to the
target. See note (1) above.
  or: or:
10log J/S = 10log Pj + 10log Gja - 10log
Pt - 10log Gt - 10log  +
10.99 dB + 20log RTx +
10.99 dB + 20log RTx |
If simplified radar equations developed in previous
sections are used: See note (2) above.
10log (J/S) = 10log Pj + 10log Gja -
10log Pt - 10log Gt - G +
+  Tx Tx  (all
factors dB) (all
factors dB) |
Target gain factor;
G = 10log = 10log  +
20log f1 + K2 (in dB) +
20log f1 + K2 (in dB) |
One-way free space loss;
 Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) |
K2 Values
(dB) |
RCS ( ) )
(units)
m 2
ft 2 |
f1
in MHz
K2 =
-38.54
-48.86 |
f1
in GHz
K2 =
21.46
11.14 |
|
K1 Values
(dB) |
Range
(units)
NM
Km
m
yd
ft |
f1
in MHz
K1 =
37.8
32.45
-27.55
-28.33
-37.87 |
f1
in GHz
K1 =
97.8
92.45
32.45
31.67
22.13 |
|
This section derives the J/S ratio from the one-way range equation
for J and the two-way range equation for S, and deals exclusively
with active (transmitting) ECM devices or systems. Furthermore,
the only purpose of the ECM considered is to prevent, delay, or
confuse the radar processing of target information.
By official definition, ECM can be either Jamming or Deception.
This may be somewhat confusing because almost any type of active
ECM is commonly called "jamming", and the calculations
of ECM signal in the radar compared to the target signal in the
radar commonly refer to the "jamming-to-signal" ratio
("J-to-S" ratio). Therefore this section uses the common
jargon and the term "jammer" refers to any ECM transmitter,
and the term "jamming" refers to any ECM transmission,
whether Deception or Concealment.
Jamming: "Official" jamming should more aptly
be called Concealment or Masking. Essentially, Concealment uses
ECM to swamp the radar receiver and hide the targets. Concealment
(Jamming) usually uses some form of noise as the transmitted ECM
signal. In this section, Concealment will be called "noise"
or "noise jamming".
Deception: Deception might be better called Forgery.
Deception uses ECM to forge false target signals that the radar
receiver accepts and processes as real targets.
"J" designates the ECM signal strength whether it
originates from a noise jammer or from a deception ECM system.
Basically, there are two different methods of employing active
ECM against hostile radars:
- Self Protection ECM
- Support ECM
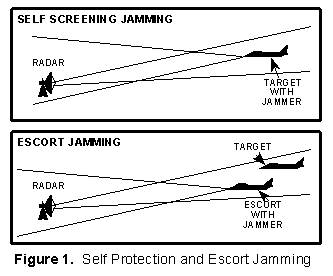 For most practical purposes, Self Protection
ECM is usually Deception and Support ECM is usually noise jamming.
As the name implies, Self Protection ECM is ECM that is used to
protect the platform that it is on. Self Protection ECM is often
called "self screening jamming", and also "DECM",
which is an acronym for either "Defensive ECM" or "Deception
ECM".
For most practical purposes, Self Protection
ECM is usually Deception and Support ECM is usually noise jamming.
As the name implies, Self Protection ECM is ECM that is used to
protect the platform that it is on. Self Protection ECM is often
called "self screening jamming", and also "DECM",
which is an acronym for either "Defensive ECM" or "Deception
ECM".
The top half of Figure 1 shows self screening jamming (DECM).
The bottom half of Figure 1 illustrates escort jamming which is
a special case of support jamming. If the escort platform is sufficiently
close to the target, the J-to-S calculations are the same as for
DECM.
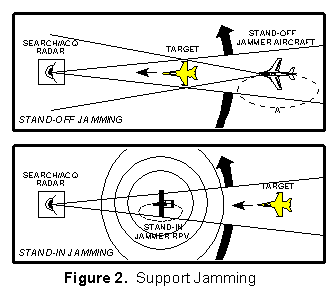 Support ECM is ECM radiated from one platform
and is used to protect other platforms. Figure 2 illustrates two
cases of support jamming - stand-off jamming (SOJ) and stand-in
jamming (SIJ). For SOJ the support jamming platform is maintaining
an orbit at a long range from the radar - usually beyond weapons
range. For SIJ, a remotely piloted vehicle is orbiting very close
to the victim radar. Obviously, the jamming power required for
the SOJ to screen a target is much greater than the jamming power
required for the SIJ to screen the same target.
Support ECM is ECM radiated from one platform
and is used to protect other platforms. Figure 2 illustrates two
cases of support jamming - stand-off jamming (SOJ) and stand-in
jamming (SIJ). For SOJ the support jamming platform is maintaining
an orbit at a long range from the radar - usually beyond weapons
range. For SIJ, a remotely piloted vehicle is orbiting very close
to the victim radar. Obviously, the jamming power required for
the SOJ to screen a target is much greater than the jamming power
required for the SIJ to screen the same target.
When factoring ECM into the radar equation, the quantities
of greatest interest are "J-to-S" and Burn- Through
Range.
"J-to-S" is the ratio of the signal strength of the
ECM signal (J) to the signal strength of the target return signal
(S). It is expressed as "J/S" and, in this section,
is always in dB. J usually (but not always) must exceed S by some
amount to be effective, therefore the desired result of a J/S
calculation in dB is a positive number. Burn-through Range is
the radar to target range where the target return signal can first
be detected through the ECM and is usually slightly farther than
crossover range where J=S. It is usually the range where the J/S
just equals the minimum effective J/S (See Burn-Through
/ Crossover Range Section).
The significance of "J-to-S" is sometimes misunderstood.
The effectiveness of ECM is not a direct mathematical function
of "J-to-S". The magnitude of the "J-to-S"
required for effectiveness is a function of the particular ECM
technique and of the radar it is being used against. Different
ECM techniques may very well require different "J-to-S"
ratios against the same radar. When there is sufficient "J-to-S"
for effectiveness, increasing it will rarely increase the effectiveness
at a given range. Because modern radars can have sophisticated
signal processing and/or ECCM capabilities, in certain radars
too much "J-to-S" could cause the signal processor to
ignore the jamming, or activate special anti-jamming modes. Increasing
"J-to-S" (or the jammer power) does, however, allow
the target aircraft to get much closer to the threat radar before
burn-through occurs, which essentially means more power is
better if it can be controlled when desired.
|
IMPORTANT NOTE: If the signal S is CW or PD and the
Jamming J is amplitude modulated, then the J used in the formula
has to be reduced from the peak value (due to sin x/x frequency
distribution). The amount of reduction is dependent upon how
much of the bandwidth is covered by the jamming signal. To get
an exact value, integrals would have to be taken over the bandwidth.
As a rule of thumb however:
- If the frequency of modulation is less than the BW of the
tracking radar reduce J/S by 10 Log(duty cycle).
- If the frequency of modulation is greater than the BW of
the tracking radar reduce J/S by 20 Log(duty cycle).
For example; if your jamming signal is square wave chopped
(50% duty cycle) at a 100 Hz rate while jamming a 1 kHz bandwidth
receiver, then the J/S is reduced by 3 dB from the maximum. If
the duty cycle was 33%, then the reduction would be 4.8 dB. If
the 50% and 33% duty cycle jamming signals were chopped at a
10 kHz (vice the 100 Hz) rate, the rule of thumb for jamming
seen by the receiver would be down 6 dB and 9.6 dB, respectively,
from the maximum since the 10 kHz chopping rate is greater than
the 1 kHz receiver BW. |
J/S for DECM vs. MONOSTATIC RADAR
Figure 3 is radar jamming visualized. The Physical concept
of Figure 3 shows a monostatic radar that is the same as Figure
1, in the Two-Way Monostatic Radar Equation
Section, and a jammer (transmitter) to radar (receiver) that
is the same as Figure 3, in the One-Way
Radar Equation Section. In other words, Figure 3 is simply
the combination of the previous two visual concepts where there
is only one receiver (the radar's).
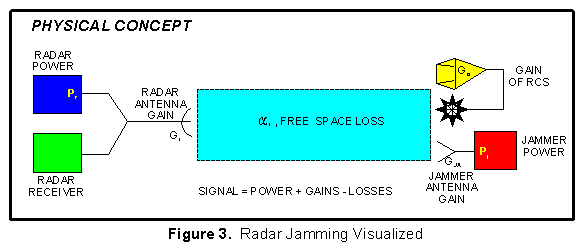
The equivalent circuit shown in Figure 4 applies to jamming
monostatic radars with either DECM or support ECM. For DECM (or
escort) v.s. a monostatic radar, the jammer is on the target and
the radar receive and transmit antennas are collocated so the
three ranges and three space loss factors ( 's)
are the same.
's)
are the same.
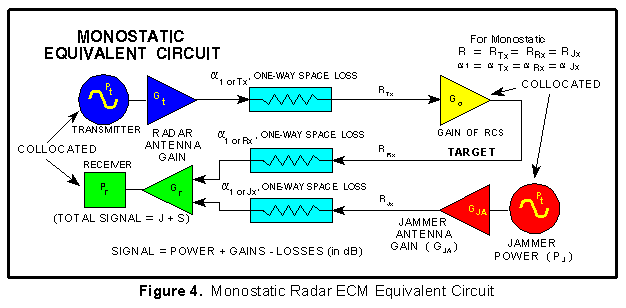
J-S Ratio (Monostatic) The ratio of the power received
(Pr1 or J) from the jamming signal transmitted from
the target to the power received (Pr2 or S) from the
radar skin return from the target equals J/S.
From the one-way range equation section:
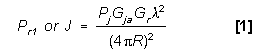
Note: To avoid having to include additional terms for these
calculations, always combine any transmission line loss with antenna
gain.
From the two-way range equation:

so:
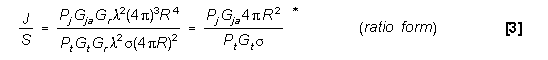 * Keep R and
* Keep R and  in the same units.
in the same units.
On reducing the above equation to log form we have:
10log J/S = 10log Pj + 10log Gja
- 10log Pt - 10log Gt - 10log  + 10log
4
+ 10log
4 + 20log R
+ 20log R  [4]
or:
[4]
or:  10log J/S = 10log
Pj+ 10log Gja - 10log Pt - 10log
Gt - 10log
10log J/S = 10log
Pj+ 10log Gja - 10log Pt - 10log
Gt - 10log  + 10.99 dB + 20log R
+ 10.99 dB + 20log R  [5]
Note: Neither f nor
[5]
Note: Neither f nor 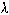 terms are part
of the final form of equation [3] and equation [5].
terms are part
of the final form of equation [3] and equation [5].
J/S Calculations (Monostatic) Using a One Way Free Space
Loss - The simplified radar equations developed in previous
sections can be used to express J/S.
From the One-way Range Equation Section:
10log (Pr1 or J) = 10log Pj +
10log Gja + 10log Gr -  (in
dB)
(in
dB)  [6]
[6]
From the Two-way Range Equation Section:
10log (Pr2 or S) = 10log Pt +
10log Gt + 10log Gr + G - 2
- 2 (in dB)
(in dB)  [7]
10log (J/S) = 10log Pj + 10log Gja
- 10log Pt - 10log Gt - G
[7]
10log (J/S) = 10log Pj + 10log Gja
- 10log Pt - 10log Gt - G +
+  (in dB)
(in dB)  [8]
[8]
Note: To avoid having to include additional terms for these
calculations, always combine any transmission line loss with antenna
gain. The 20log f 1 term in -G cancels the 20log f 1 term in
cancels the 20log f 1 term in  .
.
Target gain factor;
G = 10log = 10log  +
20log f1 + K2 (in dB) +
20log f1 + K2 (in dB) |
One-way free space loss;
 Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) |
K2 Values
(dB) |
RCS ( ) )
(units)
m 2
ft 2 |
f1
in MHz
K2 =
-38.54
-48.86 |
f1
in GHz
K2 =
21.46
11.14 |
|
K1 Values
(dB) |
Range
(units)
NM
Km
m
yd
ft |
f1
in MHz
K1 =
37.8
32.45
-27.55
-28.33
-37.87 |
f1
in GHz
K1 =
97.8
92.45
32.45
31.67
22.13 |
|
J/S for DECM vs. BISTATIC RADAR
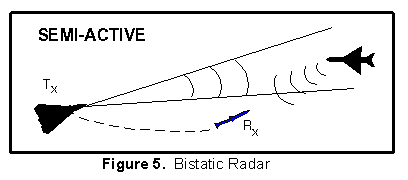 The semi-active missile illustrated in Figure
5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer
is on the target and the target to missile receiver range is the
same as the jammer to receiver range, but the radar to target
range is different. Therefore, only two of the ranges and two
of the
The semi-active missile illustrated in Figure
5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer
is on the target and the target to missile receiver range is the
same as the jammer to receiver range, but the radar to target
range is different. Therefore, only two of the ranges and two
of the  's (Figure 6.) are the same.
's (Figure 6.) are the same.
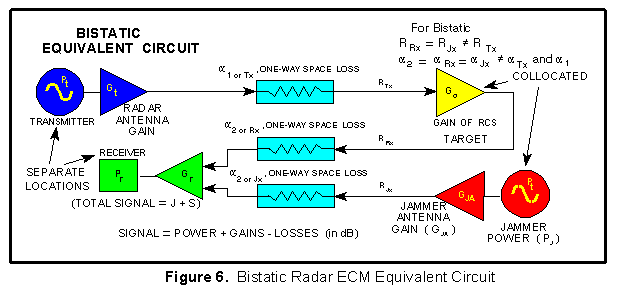
In the following equations:
 Tx = The one-way space loss from the
radar transmitter to the target for range RTx
Tx = The one-way space loss from the
radar transmitter to the target for range RTx
 Rx = The one-way space loss from the
target to the missile receiver for range RRx
Rx = The one-way space loss from the
target to the missile receiver for range RRx
Like the monostatic radar, the bistatic jamming and reflected
target signals travel the same path from the target and enter
the receiver (missile in this case) via the same antenna. In both
monostatic and bistatic J/S equations this common range cancels,
so both J/S equations are left with an RTx2
or 20 log RTx term. Since in the monostatic case RTx
= RRx and  Tx =
Tx =  Rx
, only R or
Rx
, only R or  is used in the equations. Therefore, the bistatic
J/S equations [11], [13], or [14] will work for monostatic J/S
calculations, but the opposite is only true if bistatic RTx
and
is used in the equations. Therefore, the bistatic
J/S equations [11], [13], or [14] will work for monostatic J/S
calculations, but the opposite is only true if bistatic RTx
and  Tx terms are used for R or
Tx terms are used for R or  terms
in monostatic equations [3], [5], and [8].
terms
in monostatic equations [3], [5], and [8].
The equivalent circuit shown in Figure 6 applies to jamming
bistatic radar. For DECM (or escort) vs. a bistatic radar, the
jammer is on the target and the radar receive and transmit antennas
are at separate locations so only two of the three ranges and
two of the three space loss factors ( 's) are the same.
's) are the same.
J-to-S Ratio (Bistatic) When the radar's transmit antenna
is located remotely from the receiving antenna (Figure 6), the
ratio of the power received (Pr1 or J) from the jamming
signal transmitted from the target to the power received (Pr2
or S) from the radar skin return from the target equals
J/S. For jammer effectiveness J normally has to be greater than
S.
From the One-way Range Equation Section:
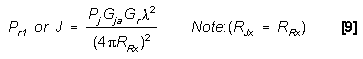
From the Two-way Range Equation Section:
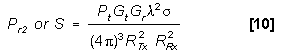
so:
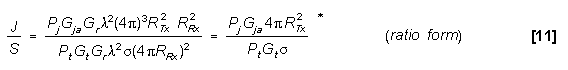 * Keep R and
* Keep R and  in the same units.
in the same units.
On reducing the above equation to log form we have:
10log J/S = 10log Pj + 10log Gja
- 10log Pt - 10log G t - 10log  + 10log
4
+ 10log
4  + 20log R Tx
+ 20log R Tx  [12]
or:
[12]
or: 10log J/S =
10log Pj + 10log Gja - 10log Pt
- 10log Gt - 10log
10log J/S =
10log Pj + 10log Gja - 10log Pt
- 10log Gt - 10log  + 10.99 dB + 20log
RTx
+ 10.99 dB + 20log
RTx  [13]
[13]
Note: To avoid having to include additional terms for these
calculations, always combine any transmission line loss with antenna
gain. Neither f nor 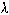 terms are part of the final
form of equation [11] and equation [13].
terms are part of the final
form of equation [11] and equation [13].
Bistatic J/S Calculations (Bistatic) Using a One Way Free
Space Loss - The simplified radar equations developed in previous
sections can be used to express J/S.
From the one way range equation:
10log (Pr1 or J) = 10log Pj
+ 10log Gja + 10log Gr -  Rx
Rx
 (all factors dB)
(all factors dB)  [14]
[14]
From the two way range equation:
10log (Pr2 or S) = 10log Pt +
10log Gt + 10log Gr + G -
-  Tx -
Tx -  Rx
Rx  (all factors dB)
(all factors dB)  [15]
10log (J/S) = 10log Pj + 10log Gja
- 10log Pt - 10log Gt - G
[15]
10log (J/S) = 10log Pj + 10log Gja
- 10log Pt - 10log Gt - G +
+  Tx
Tx  (all factors dB)
(all factors dB)
 [16]
[16]
Note: To avoid having to include additional terms for these
calculations, always combine any transmission line loss with antenna
gain. The 20log f 1 term in -G cancels the 20log f 1 term in
cancels the 20log f 1 term in  .
.
Target gain factor;
G = 10log = 10log  +
20log f1 + K2 (in dB) +
20log f1 + K2 (in dB) |
One-way free space loss;
 Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) |
K2 Values
(dB) |
RCS ( ) )
(units)
m 2
ft 2 |
f1
in MHz
K2 =
-38.54
-48.86 |
f1
in GHz
K2 =
21.46
11.14 |
|
K1 Values
(dB) |
Range
(units)
NM
Km
m
yd
ft |
f1
in MHz
K1 =
37.8
32.45
-27.55
-28.33
-37.87 |
f1
in GHz
K1 =
97.8
92.45
32.45
31.67
22.13 |
|
Saturated J/S (Monostatic) Example (Constant Power Jamming)
Assume that a 5 GHz radar has a 70 dBm signal fed through a
5 dB loss transmission line to an antenna that has 45 dB gain.
An aircraft is flying 31 km from the radar. The aft EW antenna
has -1 dB gain and a 5 dB line loss to the EW receiver (there
is an additional loss due to any antenna polarization mismatch
but that loss will not be addressed in this problem). The aircraft
has a jammer that provides 30 dBm saturated output if the received
signal is above -35 dBm. The jammer feeds a 10 dB loss transmission
line which is connected to an antenna with a 5 dB gain. If the
RCS of the aircraft is 9 m2 , what is the J/S level
received by the tracking radar?
Answer: The received signal at the jammer is the same
as the example in the One-way Radar Equation
Section, i.e. answer (1) = -32.3 dBm @ 5 GHz. Since the received
signal is above -35 dBm, the jammer will operate in the saturated
mode, and equation [5] can be used. (See Jamming
to Signal Ratio - Constant Gain Jamming Section for an example
of a jammer operating in the linear region.)
10log J/S = 10log Pj + 10log Gja
- 10log Pt - 10log Gt - 10log  + 10.99
dB + 20log R
+ 10.99
dB + 20log R
Note: the respective transmission line losses will be combined
with antenna gains, i.e. -5 + 45 = 40 dB & -10 +5 = -5 dB.
10log J/S = 30 - 5 - 70 - 40 - 9.54 + 10.99 + 89.8
= 6.25 dB @ 5 GHz*
* The answer is still 6.25 dB if the tracking radar operates
at 7 GHz provided the antenna gains and the aircraft RCS are the
same at both frequencies.
In this example, there is inadequate jamming power at each
frequency if the J/S needs to be 10 dB or greater to be effective.
One solution would be to replace the jammer with one that has
a greater power output. If the antenna of the aircraft and the
radar are not the proper polarization, additional power will also
be required (Polarization Section).
Return to: EW
& Radar Handbook Home Page | Table
of Contents
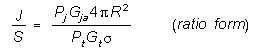

 For most practical purposes, Self Protection
ECM is usually Deception and Support ECM is usually noise jamming.
As the name implies, Self Protection ECM is ECM that is used to
protect the platform that it is on. Self Protection ECM is often
called "self screening jamming", and also "DECM",
which is an acronym for either "Defensive ECM" or "Deception
ECM".
For most practical purposes, Self Protection
ECM is usually Deception and Support ECM is usually noise jamming.
As the name implies, Self Protection ECM is ECM that is used to
protect the platform that it is on. Self Protection ECM is often
called "self screening jamming", and also "DECM",
which is an acronym for either "Defensive ECM" or "Deception
ECM". Support ECM is ECM radiated from one platform
and is used to protect other platforms. Figure 2 illustrates two
cases of support jamming - stand-off jamming (SOJ) and stand-in
jamming (SIJ). For SOJ the support jamming platform is maintaining
an orbit at a long range from the radar - usually beyond weapons
range. For SIJ, a remotely piloted vehicle is orbiting very close
to the victim radar. Obviously, the jamming power required for
the SOJ to screen a target is much greater than the jamming power
required for the SIJ to screen the same target.
Support ECM is ECM radiated from one platform
and is used to protect other platforms. Figure 2 illustrates two
cases of support jamming - stand-off jamming (SOJ) and stand-in
jamming (SIJ). For SOJ the support jamming platform is maintaining
an orbit at a long range from the radar - usually beyond weapons
range. For SIJ, a remotely piloted vehicle is orbiting very close
to the victim radar. Obviously, the jamming power required for
the SOJ to screen a target is much greater than the jamming power
required for the SIJ to screen the same target.

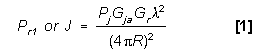

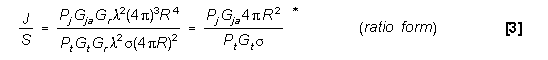
 The semi-active missile illustrated in Figure
5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer
is on the target and the target to missile receiver range is the
same as the jammer to receiver range, but the radar to target
range is different. Therefore, only two of the ranges and two
of the
The semi-active missile illustrated in Figure
5 is the typical bistatic radar which would require the target
to have self protection ECM to survive. In this case, the jammer
is on the target and the target to missile receiver range is the
same as the jammer to receiver range, but the radar to target
range is different. Therefore, only two of the ranges and two
of the