
In this section the radar equation is derived from the one-way equation (transmitter to receiver) which is then extended to the two-way radar equation. The following is a summary of the important equations to be derived here:

Figure 1 illustrates the physical concept and equivalent circuit for a target being illuminated by a monostatic radar (transmitter and receiver co-located).
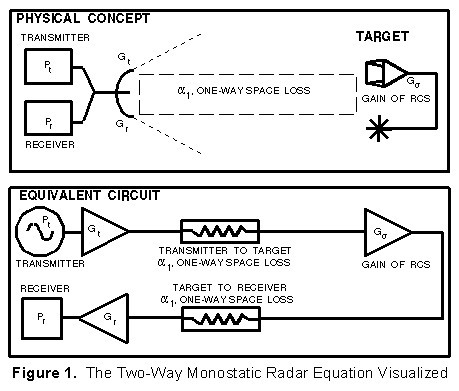
Note the similarity of Figure 1 to Figure 3 in the One-Way Radar Equation section. Transmitted power, transmitting and receiving antenna gains, and the one-way free space loss are the same as those described previously. The physical arrangement of the elements is different, of course, but otherwise the only difference is the addition of the equivalent gain of the target RCS factor.
From the One-Way Radar Equation / RF Propagation Section, the power in the receiver is:

From equation [3] in the One-Way Radar Equation / RF Propagation Section:

Similar to a receiving antenna, a radar target also intercepts
a portion of the power, but reflects (reradiates) it in the direction
of the radar. The amount of power reflected toward the radar is
determined by the Radar Cross Section (RCS) of the target. RCS
is a characteristic of the target that represents its size as
seen by the radar and has the dimensions of area (![]() ) as
shown in the RCS Section. RCS area is not
the same as physical area. But, for a radar target, the power
reflected in the radar's direction is equivalent to re-radiation
of the power captured by an antenna of area
) as
shown in the RCS Section. RCS area is not
the same as physical area. But, for a radar target, the power
reflected in the radar's direction is equivalent to re-radiation
of the power captured by an antenna of area ![]() (the
RCS). Therefore, the effective capture area (Ae) of
the receiving antenna is replaced by the RCS (
(the
RCS). Therefore, the effective capture area (Ae) of
the receiving antenna is replaced by the RCS (![]() ).
).
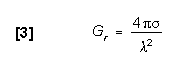 so we now have:
so we now have:![]()
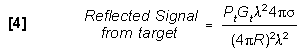
The equation for the power reflected in the radar's direction
is the same as equation [1] except that Pt Gt
, which was the original transmitted power, is replaced with the
reflected signal power from the target, from equation [4]. This
gives:
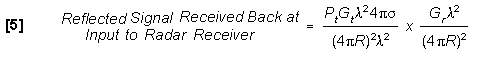
If like terms are cancelled, the two-way radar equation results.
The peak power at the radar receiver input is:
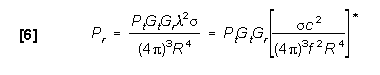
* Note: ![]() =c/f and
=c/f and ![]() = RCS. Keep
= RCS. Keep ![]() or c,
or c, ![]() , and R in the same units.
, and R in the same units.
On reducing equation [6] to log form we have:
[7] ![]() 10log Pr = 10log Pt + 10log
Gt + 10log Gr + 10log
10log Pr = 10log Pt + 10log
Gt + 10log Gr + 10log ![]() - 20log
f - 40log R - 30log 4
- 20log
f - 40log R - 30log 4 ![]() + 20log c
+ 20log c
Target Gain Factor
If Equation [5] terms are rearranged instead of cancelled,
a recognizable form results:
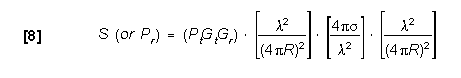
In log form:
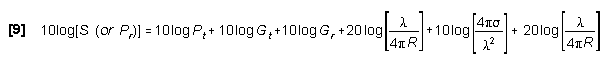
The fourth and sixth terms can each be recognized as -![]() ,
where
,
where ![]() is the one-way free space loss factor defined
in the One-Way Radar Section. The fifth term containing RCS (
is the one-way free space loss factor defined
in the One-Way Radar Section. The fifth term containing RCS (![]() )
is the only new factor, and it is the "Target Gain Factor".
)
is the only new factor, and it is the "Target Gain Factor".
In simplified terms the equation becomes:
Where ![]() and
and ![]() are as follows:
are as follows:
From the One-Way Radar Equation Section, equation [11], the space loss in dB is given by:

|
One-way free space loss, |
||
|
Range (units) |
f 1 in MHz K 1 = |
f 1 in GHz K 1 = |
| NM | 37.8 dB | 97.8 dB |
| Km | 32.45 dB | 92.45 dB |
| m | -27.55 dB | 32.45 dB |
| yd | -28.33 dB | 31.67 dB |
| ft | -37.87 dB | 22.13 dB |
While it's understood that RCS is the antenna aperture area
equivalent to an isotropically radiated target return signal,
the target gain factor represents a gain, as shown in the equivalent
circuit of Figure 1.
The Target Gain Factor expressed in dB is ![]() as
shown in equation [12].
as
shown in equation [12].
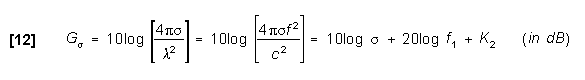

The "Target Gain Factor" (![]() ) is
a composite of RCS, frequency, and dimension conversion factors
and is called by various names: "Gain of RCS", "Equivalent
Gain of RCS", "Gain of Target Cross Section", and
in dB form "Gain-sub-Sigma".
) is
a composite of RCS, frequency, and dimension conversion factors
and is called by various names: "Gain of RCS", "Equivalent
Gain of RCS", "Gain of Target Cross Section", and
in dB form "Gain-sub-Sigma".
If frequency is given in MHz and RCS (![]() ) is
in m2, the formula for
) is
in m2, the formula for ![]() is:
is:
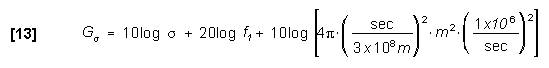
or:
|
Target gain factor, |
||
|
RCS ( (units) |
f 1 in MHz K 2 = |
f 1 in GHz K 2 = |
| m2 | -38.54 dB | 21.46 dB |
| ft2 | -48.86 dB | 11.14 dB |
In the two-way radar equation, the one-way
free space loss factor (![]() ) is used twice, once for the
radar transmitter to target path and once for the target to radar
receiver path. The radar illustrated in Figure 1 is monostatic
so the two path losses are the same and the values of the two
) is used twice, once for the
radar transmitter to target path and once for the target to radar
receiver path. The radar illustrated in Figure 1 is monostatic
so the two path losses are the same and the values of the two
![]() 's are the same.
's are the same.
If the transmission loss in Figure 1 from Pt to
Gt equals the loss from Gr to Pr
, and Gr = Gt , then equation [10] can be
written as:
The space loss factor (![]() ) and the target gain factor
(
) and the target gain factor
(![]() ) include all the necessary unit conversions
so that they can be used directly with the most common units.
Because the factors are given in dB form, they are more convenient
to use and allow calculation without a calculator when the factors
are read from a chart or nomograph.
) include all the necessary unit conversions
so that they can be used directly with the most common units.
Because the factors are given in dB form, they are more convenient
to use and allow calculation without a calculator when the factors
are read from a chart or nomograph.
Most radars are monostatic. That is, the radar transmitting and receiving antennas are literally the same antenna. There are some radars that are considered "monostatic" but have separate transmitting and receiving antennas that are co-located. In that case, equation [10] could require two different antenna gain factors as originally derived:
Note: To avoid having to include additional terms for these calculations, always combine any transmission line loss with antenna gain.
Figure 2 is the visualization of the path losses occurring with the two-way radar equation. Note: to avoid having to include additional terms, always combine any transmission line loss with antenna gain. Losses due to antenna polarization and atmospheric absorption also need to be included.
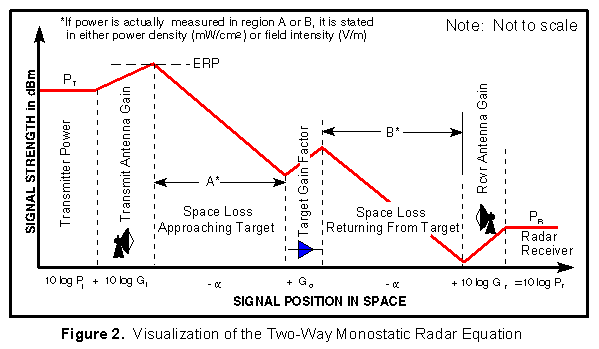
RADAR RANGE EQUATION (Two-Way Equation)
The Radar Equation is often called the "Radar Range Equation". The Radar Range Equation is simply the Radar Equation rewritten to solve for maximum Range. The maximum radar range (Rmax) is the distance beyond which the target can no longer be detected and correctly processed. It occurs when the received echo signal just equals Smin .
The Radar Range Equation is then:
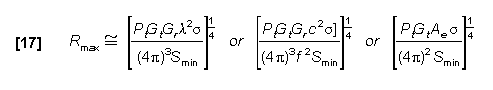
The first equation, of the three above, is given in Log form by:
[18] 40log Rmax is approximately = 10log
Pt + 10log Gt + 10log Gr + 10log
![]() - 10log Smin - 20log f -
30log 4
- 10log Smin - 20log f -
30log 4 ![]() + 20log c
+ 20log c
As shown previously, Since K1 = 20log [(4 ![]() /c)
times conversion units if not in m/sec, m, and Hz], we have:
/c)
times conversion units if not in m/sec, m, and Hz], we have:
[19] 10log Rmax is approximately = 1/4 [10log
Pt + 10log Gt + 10log Gr + 10log
![]() - 10log Smin - 20log f
1 - K1 - 10.99 dB]
- 10log Smin - 20log f
1 - K1 - 10.99 dB]
If you want to convert back from dB, then![]()
Where M dB is the resulting number within the brackets of equation 19.
From the Receiver Sensitivity / Noise Section, Smin is related to the noise factors by:
The Radar Range Equation for a tracking radar (target continuously in the antenna beam) becomes:
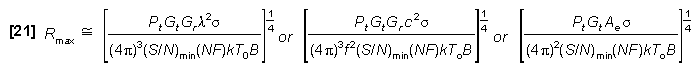
Pt in equations [17], [19], and [21] is the peak power of a CW or pulse signal. For pulse signals these equations assume the radar pulse is square. If not, there is less power since Pt is actually the average power within the pulse width of the radar signal. Equations [17] and [19] relate the maximum detection range to Smin , the minimum signal which can be detected and processed (the receiver sensitivity). The bandwidth (B) in equations [20] and [21] is directly related to Smin . B is approximately equal to 1/PW. Thus a wider pulse width means a narrower receiver bandwidth which lowers Smin , assuming no integration.
One cannot arbitrarily change the receiver bandwidth, since it has to match the transmitted signal. The "widest pulse width" occurs when the signal approaches a CW signal (see Modulation Section). A CW signal requires a very narrow bandwidth (approximately 100 Hz). Therefore, receiver noise is very low and good sensitivity results (see Receiver Sensitivity Section). If the radar pulse is narrow, the receiver filter bandwidth must be increased for a match (, i.e. a 1 µsec pulse requires a bandwidth of approximately 1 MHz. This increases receiver noise and decreases sensitivity.
If the radar transmitter can increase its PRF (decreasing PRI) and its receiver performs integration over time, an increase in PRF can permit the receiver to "pull" coherent signals out of the noise thus reducing S/Nmin thereby increasing the detection range. Note that a PRF increase may limit the maximum range due to the creation of overlapping return echoes (see the Propagation Time / Resolution Section).
There are also other factors that limit the maximum practical detection range. With a scanning radar, there is loss if the receiver integration time exceeds the radar's time on target. Many radars would be range limited by line-of-sight/radar horizon (see the Radar Horizon Section) well before a typical target faded below Smin. Range can also be reduced by losses due to antenna polarization and atmospheric absorption (see Sections on Polarization and RF Atmospheric Absorption).
Two-Way Radar Equation (Example)
Assume that a 5 GHz radar has a 70 dBm (10 kilowatt) signal fed through a 5 dB loss transmission line to a transmit/receive antenna that has 45 dB gain. An aircraft that is flying 31 km from the radar has an RCS of 9 m2. What is the signal level at the input to the radar receiver? (There is an additional loss due to any antenna polarization mismatch but that loss will not be addressed in this problem). This problem continues in other sections.
Answer:
Starting with: ![]() 10log
S = 10log Pt + 10log Gt + 10log Gr
+
10log
S = 10log Pt + 10log Gt + 10log Gr
+ ![]() -2
-2![]() (in dB)
(in dB)
We know that:![]()
![]() = 20log f
R + K1 = 20log (5x31) + 92.44 = 136.25 dB
= 20log f
R + K1 = 20log (5x31) + 92.44 = 136.25 dB
and that:![]()
![]() = 10log
= 10log![]() + 20log
f1 + K2 = 10log 9 + 20log 5 + 21.46
= 44.98 dB (see Table 1)
+ 20log
f1 + K2 = 10log 9 + 20log 5 + 21.46
= 44.98 dB (see Table 1)
(Note: The aircraft transmission line losses (-5 dB) will be combined with the antenna gain (45 dB) for both receive and transmit paths of the radar)
So substututing in, we have: ![]() 10log
S = 70 + 40 + 40 + 44.98 - 2(136.25) = -77.52 dBm @ 5 GHz
10log
S = 70 + 40 + 40 + 44.98 - 2(136.25) = -77.52 dBm @ 5 GHz
The answer changes to -80.44 dBm if the tracking radar operates at 7 GHz provided the antenna gains and the aircraft RCS are the same at both frequencies.
![]() = 20log (7x31) + 92.44 = 139.17 dB,
= 20log (7x31) + 92.44 = 139.17 dB, ![]()
![]() = 10log 9 + 20log 7 + 21.46 = 47.9 dB (see Table 1)
= 10log 9 + 20log 7 + 21.46 = 47.9 dB (see Table 1)
10log S = 70 + 40 + 40 + 47.9 - 2(139.17) = -80.44 dBm @ 7 GHz
| Frequency (GHz) |
|
||||||
| 0.05 | 5 | 9 | 10 | 100 | 1,000 | 10,000 | |
| 1 GHz | 8.46 | 28.46 | 31.0 | 31.46 | 41.46 | 51.46 | 61.46 |
| 5 GHz | 22.44 | 42.44 | 44.98* | 45.44 | 55.44 | 65.44 | 75.44 |
| 7 GHz | 25.36 | 45.36 | 47.9* | 48.36 | 58.36 | 68.36 | 78.36 |
| 10 GHz | 28.46 | 48.46 | 51.0 | 51.46 | 61.46 | 71.46 | 81.46 |
| 20 GHz | 34.48 | 54.48 | 57.02 | 57.48 | 67.48 | 77.4 | 87.48 |
As shown in equation [17] S min-1 is proportional to Rmax 4 Therefore, -10 log Smin is proportional to 40 logR max and Table 2 below results:
% Range Increase: Range + (% Range Increase) x Range
= New Range
i.e., for a 12 dB sensitivity increase, 500 miles +100% x 500
miles = 1,000 miles
Range Multiplier: Range x Range Multiplier = New Range
i.e., for a 12 dB sensitivity increase 500 miles x 2 = 1,000 miles
|
dB Sensitivity Increase |
% Range Increase |
Range Multiplier |
dB Sensitivity Increase |
% Range Increase |
Range Multiplier |
|
| + 0.5 | 3 | 1.03 | 10 | 78 | 1.78 | |
| 1.0 | 6 | 1.06 | 11 | 88 | 1.88 | |
| 1.5 | 9 | 1.09 | 12 | 100 | 2.00 | |
| 2 | 12 | 1.12 | 13 | 111 | 2.11 | |
| 3 | 19 | 1.19 | 14 | 124 | 2.24 | |
| 4 | 26 | 1.26 | 15 | 137 | 2.37 | |
| 5 | 33 | 1.33 | 16 | 151 | 2.51 | |
| 6 | 41 | 1.41 | 17 | 166 | 2.66 | |
| 7 | 50 | 1.50 | 18 | 182 | 2.82 | |
| 8 | 58 | 1.58 | 19 | 198 | 2.98 | |
| 9 | 68 | 1.68 | 20 | 216 | 3.16 |
As shown in equation [17] Smin-1 is proportional to Rmax4 Therefore, -10 log Smin is proportional to 40 logRmax and Table 3 below results:
% Range Decrease: Range - (% Range Decrease) x Range
= New Range
i.e., for a 12 dB sensitivity decrease, 500 miles - 50% x 500
miles = 250 miles
Range Multiplier: Range x Range Multiplier = New Range
i.e., for a 12 dB sensitivity decrease 500 miles x 0.5 = 250 miles
|
dB Sensitivity Decrease |
% Range Decrease |
Range Multiplier |
dB Sensitivity Decrease |
% Range Decrease |
Range Multiplier |
|
| - 0.5 | 3 | 0.97 | -10 | 44 | 0.56 | |
| - 1.0 | 6 | 0.94 | - 11 | 47 | 0.53 | |
| - 1.5 | 8 | 0.92 | - 12 | 50 | 0.50 | |
| - 2 | 11 | 0.89 | - 13 | 53 | 0.47 | |
| - 3 | 16 | 0.84 | - 14 | 55 | 0.45 | |
| - 4 | 21 | 0.79 | - 15 | 58 | 0.42 | |
| - 5 | 25 | 0.75 | - 16 | 60 | 0.40 | |
| - 6 | 29 | 0.71 | - 17 | 62 | 0.38 | |
| - 7 | 33 | 0.67 | - 18 | 65 | 0.35 | |
| - 8 | 37 | 0.63 | - 19 | 67 | 0.33 | |
| - 9 | 40 | 0.60 | - 20 | 68 | 0.32 |