JAMMING TO SIGNAL (J/S) RATIO
CONSTANT
GAIN [LINEAR] JAMMING
The following is a summary of equations developed in
this section:
Since the jammer on the target is amplifying the received radar
signal before transmitting it back to the radar, both J and S
experience the two way range loss. Figure 1 shows that the range
for both the signal and constant gain jamming have a slope that
is 40 dB per decade.
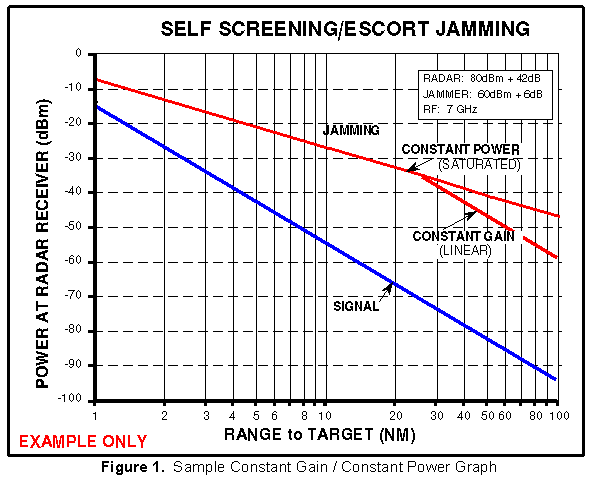
Once the jammer output reaches maximum power, that power is
constant and the jamming slope changes to 20 dB per decade since
it is only a function of one way space loss and the J/S equations
for constant power (saturated) jamming must be used.
Normally the constant gain (linear) region of a repeater jammer
occurs only at large distances from the radar and the constant
power (saturated) region is reached rapidly as the target approaches
the radar. When a constant gain jammer is involved it may be necessary
to plot jamming twice - once using J from equation [1] in the
J/S - Constant Power (Saturated) Section
and once using the constant gain (linear) equation [4] (shown
later), as in the example shown in Figure 1.
CONSTANT GAIN SELF PROTECTION DECM
Most jammers have a constant power output - that is, they always
transmit the maximum available power of the transmitter (excepting
desired ECM modulation). Some jammers also have a constant gain
(linear) region. Usually these are coherent repeaters that can
amplify a low level radar signal to a power that is below the
level that results in maximum available (saturated) power output.
At some radar to target range, the input signal is sufficiently
high that the full jammer gain would exceed the maximum available
power and the jammer ceases to be constant gain and becomes constant
power.
To calculate the power output of a constant gain jammer where:
SRj = The Radar signal at the jammer input
(receive antenna terminals)
Gja(Rx)
= The Gain of the jammer receive antenna
Gj
= The gain of the jammer
 Tx
= The one-way free space loss from the radar to the target
Tx
= The one-way free space loss from the radar to the target
PjCG = The jammer constant gain power output
Pj = The maximum jammer power output
LR = The jammer receiving line loss; combine
with antenna gain Gja(Rx)
From equation [10], in the One-Way Radar
Equation Section, calculate the radar power received by the
jammer.
10log SRj = 10log Pt + 10log Gt
-  Tx + 10log Gja(Rx)
Tx + 10log Gja(Rx)  (factors in dB)
(factors in dB)  [1]
[1]
The jammer constant gain power output is:
10log PjCG = 10log SRj + 10log Gja
 [2]
[2]
and, by definition: PjCG < or = Pj
 [3]
[3]
MONOSTATIC
The equivalent circuit shown in Figure 2 is different from
the constant power equivalent circuit in Figure 4 in the J/S
- Constant Power (saturated) Section. With constant gain,
the jamming signal experiences the gain of the jammer and its
antennas plus the same space loss as the radar signal.
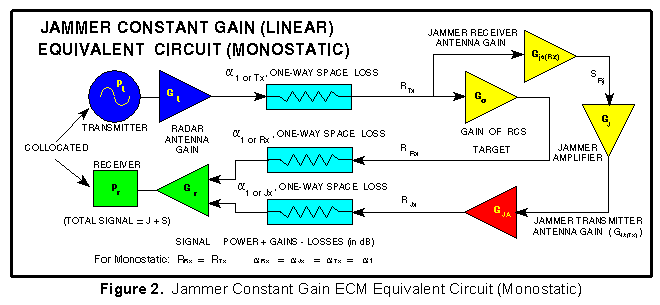
To calculate J, the one way range equation is used twice:

 [4]
From the Two-way Range Equation
Section:
[4]
From the Two-way Range Equation
Section: 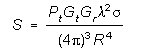
 [5]
[5]
Terms cancel when combined: 
 [6]
[6]
Or in dB form: 10log J/S = 10log Gja(Rx)
+ 10log Gj + 10log Gja(Tx) - 10log (4
 /
/ 2
)
2
)  [7]
[7]
Since the last term can be recognized as minus G from equation [10] in the Two-Way Radar
Equation (Monostatic) Section, where the target gain factor,
G
from equation [10] in the Two-Way Radar
Equation (Monostatic) Section, where the target gain factor,
G = 10log (4
= 10log (4
 /
/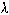 2
) = 10log (4
2
) = 10log (4
 f 2 /c 2 ), it follows
that:
f 2 /c 2 ), it follows
that:
10log J/S = 10log Gja(Rx) + 10log Gj
+ 10log Gja(Tx) - G
 (factors
in dB)
(factors
in dB)  [8]
[8]
Target gain factor, G = 10log = 10log
 + 20log f1 + K2
(in dB) + 20log f1 + K2
(in dB) |
|
K2 Values (dB) |
RCS ( ) )
(units) |
f1 in MHz
K2 = |
f1 in GHz
K2 = |
|
m 2 |
-38.54 |
21.46 |
|
ft 2 |
-48.86 |
11.14 |
|
BISTATIC
The bistatic equivalent circuit shown in Figure 3 is different
from the monostatic equivalent circuit shown in Figure 2 in that
the receiver is separately located from the transmitter, RTx
does not equal RRx or RJx and G will be different since the RCS (
will be different since the RCS ( ) varies with
aspect angle.
) varies with
aspect angle.
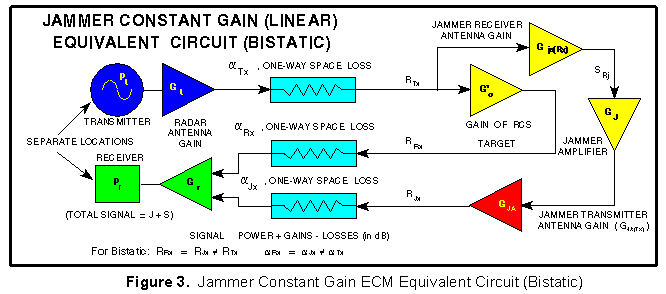
To calculate J, the one way range equation is used twice:

 (RJx
= RRx)
(RJx
= RRx)  [9]
[9]
From the two way range equation:
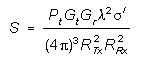 (
( ' is bistatic RCS)
' is bistatic RCS)
 [10]
[10]
Terms cancel when combined: 
 [11]
[11]
Or in dB form: 10log J/S = 10log Gja(Rx)
+ 10log Gj + 10log Gja(Tx) - 10log (4
 '/
'/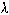 2
)
2
)  [12]
[12]
Since the last term can be recognized as minus G from equation [10] in the Two-Way Radar Equation (monostatic)
Section, where the target gain factor, G
from equation [10] in the Two-Way Radar Equation (monostatic)
Section, where the target gain factor, G = 10log (4
= 10log (4
 '/
'/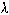 2 ) = 10log (4
2 ) = 10log (4
 'f
2 /c 2 ), it follows that:
'f
2 /c 2 ), it follows that:
10log = 10log Gja(Rx) + 10log Gj + 10log
Gja(Tx) - G '
' (factors
in dB)
(factors
in dB)  [13]
[13]
Linear J/S (Monostatic) Example (Linear Power Jamming)
Assume that a 5 GHz radar has a 70 dBm signal fed through a
5 dB loss transmission line to an antenna that has 45 dB gain.
An aircraft that is flying 31 km from the radar has an aft EW
antenna with -1 dB gain and a 5 dB line loss to the EW receiver
(there is an additional loss due to any antenna polarization mismatch
but that loss will not be addressed in this problem). The received
signal is fed to a jammer with a gain of 60 dB, feeding a 10 dB
loss transmission line which is connected to an antenna with 5
dB gain.
If the RCS of the aircraft is 9 m2 , what is the
J/S level received at the input to the receiver of the tracking
radar?
Answer:
10log J/S = 10log Gja(Rx) + 10log Gj
+ 10log Gja(Tx) - G
G = 10log
= 10log  + 20log f1
+ K2 = 10log 9 + 20log 5 + 21.46 = 44.98 dB
+ 20log f1
+ K2 = 10log 9 + 20log 5 + 21.46 = 44.98 dB
Note: The respective transmission line losses will be combined
with antenna gains, i.e. -1 -5 = -6 dB and -10 + 5 = -5 dB
10log J/S = -6 + 60 - 5 - 44.98 = 4.02 dB @ 5 GHz
The answer changes to 1.1 dB if the tracking radar operates
at 7 GHz provided the antenna gains and aircraft RCS are the same
at both 5 and 7 GHz.
G = 10log 9 + 20log 7 + 21.46 = 47.9 dB
= 10log 9 + 20log 7 + 21.46 = 47.9 dB
10log J/S = -6 + 60 - 5 - 47.9 = 1.1 dB @ 7 GHz
Separate J (-73.5 dBm @ 5 GHz and -79.34 dBm @ 7 GHz) and S
(-77.52 dBm @ 5 GHz and -80.44 dBm @ 7 GHz) calculations for this
problem are provided in the One-Way and Two-Way Radar Equation
Sections, respectively. A saturated gain version of this problem
is provided in the J/S Ratio - Constant Power (Saturated) Jamming
Section.
Return to: EW
& Radar Handbook Home Page | Table
of Contents

![]()
![]() /
/![]() 2
)
2
)![]() (dB)
(dB)![]() and
and ![]() in
same units. Note:
in
same units. Note: ![]() = c/f
= c/f


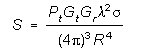



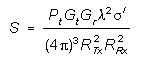 (
(