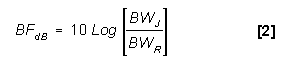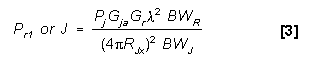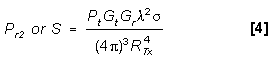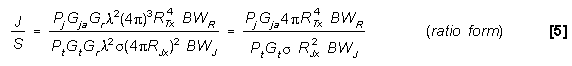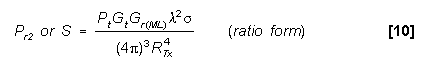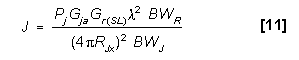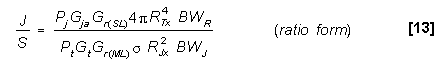SUPPORT JAMMING
The following table contains a summary of equations
developed in this section:
MAIN LOBE JAMMING TO SIGNAL (J/S) RATIO (For SOJ/SIJ)
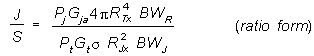  or (in dB): or (in dB):
10log J/S = 10logPj -
10log[BWj/BWR] + 10logGja -
10logPt - 10logGt - 10log +
10.99 dB + 40logRTx - 20logRJx +
10.99 dB + 40logRTx - 20logRJx |
If simplified radar equations developed in previous
sections are used (in dB):
10log J/S = 10log Pj
- BF + 10log Gja -  Jx
- 10log Pt - 10log Gt - G Jx
- 10log Pt - 10log Gt - G + 2
+ 2  |
SIDE LOBE JAMMING TO SIGNAL (J/S) RATIO (For SOJ/SIJ)
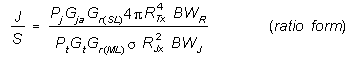 or (in dB): or (in dB):
10log J/S = 10logPj - BF + 10logGja
+ 10logGr(SL) - 10logPt - 10logGt
- 10logGr(ML) - 10log  + 10.99 dB +
40logRTx - 20logRJx + 10.99 dB +
40logRTx - 20logRJx |
If simplified radar equations developed in previous
sections are used (in dB):
10log
J/S = 10logPj - BF + 10logGja + 10logGr(SL)
-  Jx - 10logPt - 10logGt
- 10logGr(ML) - G Jx - 10logPt - 10logGt
- 10logGr(ML) - G + 2 + 2 |
RJx
RTx
BF
Gr(SL)
Gr(ML)
 JX JX
 |
Range from the support jammer transmitter to
the radar receiver
Range between the radar and the target
10 Log of the ratio of BWJ of the noise jammer to
BWR of the radar receiver
Side lobe antenna gain
Main lobe antenna gain
One way free space loss between SOJ transmitter and radar receiver
One way space loss between the radar and the target |
|
Target gain factor;
G = 10log = 10log  + 20log f1
+ K2 (in dB) + 20log f1
+ K2 (in dB) |
One-way free space loss;
 Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) Tx or Rx = 20log (f1 RTx
or Rx) + K1 (in dB) |
K2 Values
(dB) |
RCS ( ) )
(units)
m 2
ft 2 |
f1
in MHz
K2 =
-38.54
-48.86 |
f1
in GHz
K2 =
21.46
11.14 |
|
K1 Values
(dB) |
Range
(units)
NM
Km
m
yd
ft |
f1
in MHz
K1 =
37.8
32.45
-27.55
-28.33
-37.87 |
f1
in GHz
K1 =
97.8
92.45
32.45
31.67
22.13 |
|
Support jamming adds a few geometric complexities. A stand-off
jammer (SOJ) platform usually uses high gain, directional antennas.
Therefore, the jamming antenna must not only be pointed at the
victim radar, but there must be alignment of radar, targets, and
SOJ platform for the jamming to be effective. Two cases will be
described, main lobe-jamming and side-lobe jamming.
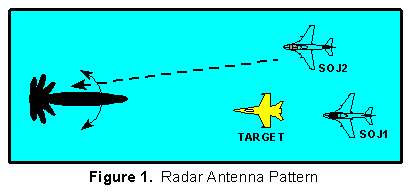 Support jamming is usually applied against
search and acquisition radars which continuously scan horizontally
through a volume of space. The scan could cover a sector or a
full 360°. The horizontal antenna pattern of the radar will
exhibit a main lobe and side lobes as illustrated in Figure 1.
The target is detected when the main lobe sweeps across it. For
main lobe jamming, the SOJ platform and the target(s) must be
aligned with the radar's main lobe as it sweeps the target(s).
Support jamming is usually applied against
search and acquisition radars which continuously scan horizontally
through a volume of space. The scan could cover a sector or a
full 360°. The horizontal antenna pattern of the radar will
exhibit a main lobe and side lobes as illustrated in Figure 1.
The target is detected when the main lobe sweeps across it. For
main lobe jamming, the SOJ platform and the target(s) must be
aligned with the radar's main lobe as it sweeps the target(s).
For side lobe jamming, the SOJ platform may be aligned with
one or more of the radar's side lobes when the main lobe sweeps
the target. The gain of a radar's side lobes are many tens of
dB less (usually more than 30 dB less) than the gain of the main
lobe, so calculations of side lobe jamming must use the gain of
the side lobe for the radar receive antenna gain, not the gain
of the main lobe. Also, because many modern radars employ some
form of side lobe blanking or side lobe cancellation, some knowledge
of the victim radar is required for the employment of side lobe
jamming.
All radar receivers are frequency selective. That is, they
are filters that allow only a narrow range of frequencies into
the receiver circuitry. DECM, by definition, creates forgeries
of the real signal and, ideally, are as well matched to the radar
receiver as the real signal. On the other hand, noise jamming
probably will not match the radar receiver bandwidth characteristics.
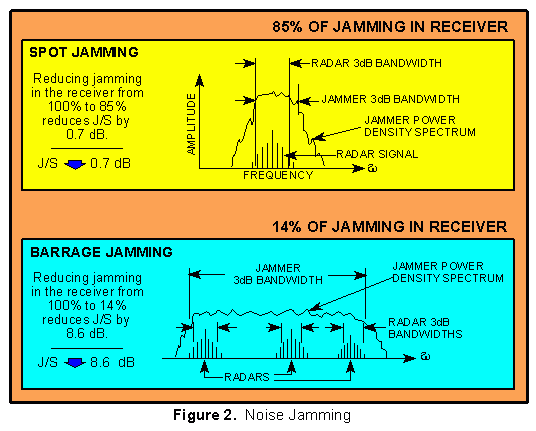
Noise jamming is either spot jamming or barrage jamming. As illustrated
in Figure 2, spot jamming is simply narrowing the bandwidth of
the noise jammer so that as much of the jammer power as possible
is in the radar receiver bandwidth. Barrage jamming is using a
wide noise bandwidth to cover several radars with one jammer or
to compensate for any uncertainty in the radar frequency. In both
cases some of the noise power is "wasted" because it
is not in the radar receiver filter.
In the past, noise jammers were often described as having so
many "watts per MHz". This is nothing more than the
power of the noise jammer divided by the noise bandwidth. That
is, a 500 watt noise jammer transmitting a noise bandwidth of
200 MHz has 2.5 watts/MHz. Older noise jammers often had noise
bandwidths that were difficult, or impossible, to adjust accurately.
These noise jammers usually used manual tuning to set the center
frequency of the noise to the radar frequency. Modern noise jammers
can set on the radar frequency quite accurately and the noise
bandwidth is selectable, so the noise bandwidth is more a matter
of choice than it used to be, and it is possible that all of the
noise is placed in the victim radar's receiver.
If, in the example above, the 500 watt noise jammer were used
against a radar that had a 3 MHz receiver bandwidth, the noise
jammer power applicable to that radar would be:
3 MHz x 2.5 watts/MHz = 7.5 watts or 38.75 dBm [1]
[1]
The calculation must be done as shown in equation [1] - multiply
the watts/MHz by the radar bandwidth first and then convert to
dBm. You can't convert to dBm/MHz and then multiply. (See derivation
of dB in Decibel Section)
An alternate method for dB calculations is to use the bandwidth
reduction factor (BF). The BF is:
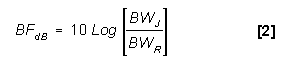
where: BWJ is the bandwidth of the noise jammer,
and BWR is the bandwidth of the radar receiver.
The power of the jammer in the jamming equation (PJ)
can be obtained by either method. If equation [1] is used then
PJ is simply 38.75 dBm. If equation [2] is used then
the jamming equation is written using (PJ - BF). The
following discussion uses the second method. Whichever method
is used, it is required that BWJ > or = BWR.
If BWJ < BWR, then all the available
power is in the radar receiver and equation [1] does not apply
and the BF = 0.
|
Note: To avoid having to include additional
terms for the following calculations, always combine any transmission
line loss with antenna gain. |
MAIN LOBE STAND-OFF / STAND-IN JAMMING
The equivalent circuit shown in Figure 3 applies to main lobe
jamming by a stand-off support aircraft or a stand-in RPV.
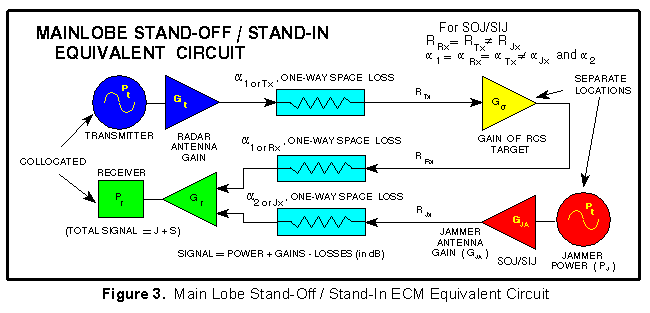
Since the jammer is not on the target aircraft, only two of
the three ranges and two of the three space loss factors ( 's)
are the same. Figure 3 differs from the J/S monostatic equivalent
circuit shown in Figure 4 in the Constant-Power
(Saturated) Jamming Section in that the space loss from the
jammer to the radar receiver is different.
's)
are the same. Figure 3 differs from the J/S monostatic equivalent
circuit shown in Figure 4 in the Constant-Power
(Saturated) Jamming Section in that the space loss from the
jammer to the radar receiver is different.
The equations are the same for both SOJ and SIJ. From the one
way range equation in the One-Way Radar
Equation Section, and with inclusion of BF losses:
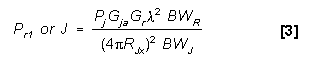
From the two-way range equation in the Two-Way
Radar Equation (Monostatic) Section:
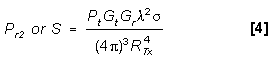 so
so
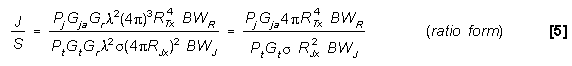
Note:
Keep R and  in the same units.
in the same units.
Converting to dB and using 10 log 4 = 10.99 dB:
= 10.99 dB:
10log J/S = 10logPj - 10log[BWj/BWR]
+ 10logGja - 10logPt - 10logGt
- 10log + 10.99 dB + 40logRTx - 20logRJx
[6]
+ 10.99 dB + 40logRTx - 20logRJx
[6]
If the simplified radar equation is used, the free space loss
from the SOJ/SIJ to the radar receiver is  Jx,
then equation [7] is the same as monostatic equation [6] in the
Constant Power (Saturated) Jamming Section
except
Jx,
then equation [7] is the same as monostatic equation [6] in the
Constant Power (Saturated) Jamming Section
except  Jx replaces
Jx replaces  , and the bandwidth
reduction factor [BF] losses are included:
, and the bandwidth
reduction factor [BF] losses are included:
10log J = 10log Pj - BF + 10log Gja +
10log Gr -  Jx
Jx (factors in dB)
(factors in dB) [7]
[7]
Since the free space loss from the radar to the target and
return is the same both ways,  Tx =
Tx =
 Rx =
Rx =  , equation [8]
is the same as monostatic equation [7] in the Constant
Power (Saturated) Jamming Section .
, equation [8]
is the same as monostatic equation [7] in the Constant
Power (Saturated) Jamming Section .
10log S = 10log Pt + 10log Gt + 10log
Gr + G - 2
- 2 
 (factors in dB)
(factors in dB)  [8]
[8]
and
10log J/S = 10log Pj - BF + 10log Gja
-  Jx - 10log Pt - 10log Gt
- G
Jx - 10log Pt - 10log Gt
- G + 2
+ 2 
 (factors
in dB)
(factors
in dB)  [9]
[9]
Notice that unlike equation [8] in the Constant
Power (Saturated) Jamming Section , there are two different
 's in [9] because the signal paths are different.
's in [9] because the signal paths are different.
SIDE LOBE STAND-OFF / STAND-IN JAMMING
The equivalent circuit shown in Figure 4. It differs from Figure
3, (main lobe SOJ/SIJ) in that the radar receiver antenna gain
is different for the radar signal return and the jamming.
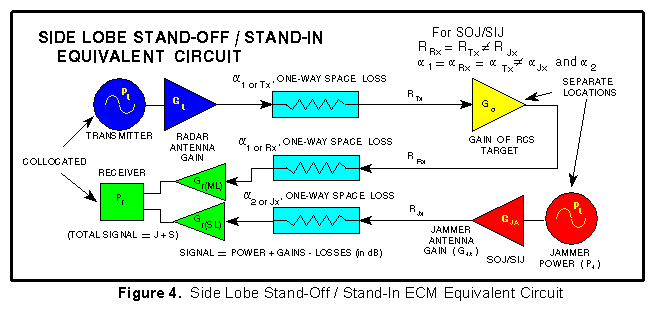
To calculate side lobe jamming, the gain of the radar antenna's
side lobes must be known or estimated. The gain of each side lobe
will be different than the gain of the other side lobes. If the
antenna is symmetrical, the first side lobe is the one on either
side of the main lobe, the second side lobe is the next one on
either side of the first side lobe, and so on. The side lobe gain
is GSLn where the 'n' subscript denotes side lobe number:
1, 2, ..., n.
The signal is the same as main lobe equations [4] and [8],
except Gr = Gr(ML)
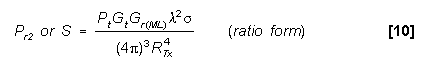
If simplified radar equations are used:
10log S = 10log Pt + 10log Gt + 10log
Gr(ML) + G - 2
- 2 (factors
in dB)
(factors
in dB)
The jamming equation is the same as main lobe equations [3]
and [7] except Gr = Gr(SL) so:
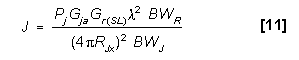
10log J = 10log Pj - BF + 10log Gja +
10log Gr(SL) -  Jx
Jx  (factors
in dB)
(factors
in dB)  [12]
[12]
so
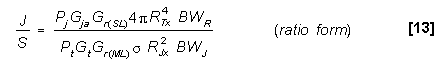
Note:
keep R and  in same units.
in same units.
Converting to dB and using 10log 4 = 10.99 dB:
= 10.99 dB:
10log J/S = 10logPj - BF + 10logGja +
10logGr(SL) - 10logPt - 10logGt
- 10logGr(ML) - 10log  + 10.99 dB + 40logRTx
- 20logRJx (factors in dB)
+ 10.99 dB + 40logRTx
- 20logRJx (factors in dB)  [14]
[14]
If simplified radar equations are used:
10log J/S = 10logPj - BF + 10logGja +
10logGr(SL) -  Jx - 10logPt
- 10logGt - 10logGr(ML) - G
Jx - 10logPt
- 10logGt - 10logGr(ML) - G + 2
+ 2 (in dB)
(in dB)  [15]
[15]
Return to: EW
& Radar Handbook Home Page | Table
of Contents
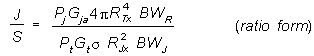
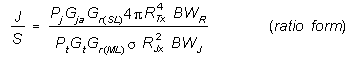 or (in dB):
or (in dB): Support jamming is usually applied against
search and acquisition radars which continuously scan horizontally
through a volume of space. The scan could cover a sector or a
full 360°. The horizontal antenna pattern of the radar will
exhibit a main lobe and side lobes as illustrated in Figure 1.
The target is detected when the main lobe sweeps across it. For
main lobe jamming, the SOJ platform and the target(s) must be
aligned with the radar's main lobe as it sweeps the target(s).
Support jamming is usually applied against
search and acquisition radars which continuously scan horizontally
through a volume of space. The scan could cover a sector or a
full 360°. The horizontal antenna pattern of the radar will
exhibit a main lobe and side lobes as illustrated in Figure 1.
The target is detected when the main lobe sweeps across it. For
main lobe jamming, the SOJ platform and the target(s) must be
aligned with the radar's main lobe as it sweeps the target(s).